PERIMETER AND AREA PROBLEMS ON CUSTOMARY UNITS OF LENGTH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Find the perimeter and the area of the rectangle. When possible, express your answer as a whole or mixed number.
Problem 1 :
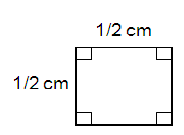
Solution :
Area of the square = (side)2
= (1/2)2
= 1/4 cm2
So, area of the square is 1/4 cm2
Perimeter of the square = 4 × side
= 4 × 1/2
= 4/2
= 2 cm
So, perimeter of the square is 2 cm.
Problem 2 :
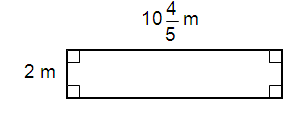
Solution :
By observing the figure,
Length = 54/5
Width = 2 m
Area of the rectangle = l × w
= (54/5) × 2
= 10.8 × 2
= 21.6 m2
So, area of the rectangle is 21.6 m2
Perimeter of the rectangle = 2 × (l + w)
= 2 × (54/5 + 2)
= 2 × (10.8 + 2)
= 2 × 12.8
= 25.6 m
So, perimeter of the rectangle is 25.6 m.
Problem 3 :
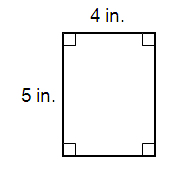
Solution :
By observing the figure,
Length = 4 in.
Width = 5 in.
Area of the rectangle = l × w
= 4 × 5
= 20 in2.
So, area of the rectangle is 20 in2.
Perimeter of the rectangle = 2 × (l + w)
= 2 × (4 + 5)
= 2 × 9
= 18 in.
So, perimeter of the rectangle is 18 in.
Problem 4 :
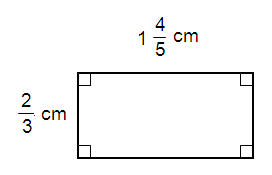
Solution :
By observing the figure,
Length = 9/5 cm
Width = 2/3 cm
Area of the rectangle = l × w
= 9/5 × 2/3
= 18/15
= 6/5 cm2
So, area of the rectangle is 6/5 cm2.
Perimeter of the rectangle = 2 × (l + w)
= 2 × (9/5 + 2/3)
= 2 × (9/5 × 3/3 + 2/3 × 5/5)
= 2 × (27/15 + 10/15)
= 2 × (37/15)
= 74/15 cm
So, perimeter of the rectangle is 74/15 cm.
Find the side length of the rectangle.
Problem 5 :
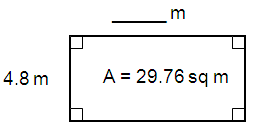
Solution :
By observing the figure,
Length = ___ m
Width = 4.8 m
area of the rectangle = 29.76 sq m
Area of the rectangle = l × w
29.76 = l × 4.8
l = 29.76/4.8
l = 6.2 m
So, side length of the rectangle is 6.2 m.
Perimeter of the rectangle = 2 × (l + w)
= 2 × (6.2 + 4.8)
= 2 × 11
= 22 m
So, perimeter of the rectangle is 22 m.
Problem 6 :
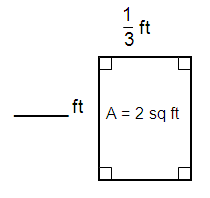
Solution :
By observing the figure,
Length = 1/3 ft
Width = ___ ft
area of the rectangle = 2 sq ft
Area of the rectangle = l × w
2 = 1/3 × w
2= w/3
w = 6 ft
So, width of the rectangle is 6 ft.
Perimeter of the rectangle = 2 × (l + w)
= 2 × (1/3 + 6)
= 2 × (1/3 + 18/3)
= 2 × (19/3)
= 38/3
So, perimeter of the rectangle is 38/3 ft.
Problem 7 :
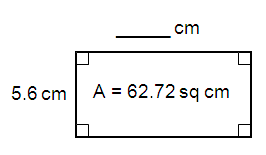
Solution :
By observing the figure,
Length = _____ cm
Width = 5.6 cm
area of the rectangle = 62.72 sq cm
Area of the rectangle = l × w
62.72 = l × 5.6
l = 62.72/5.6
l = 11.2
So, length of the rectangle is 11.2 cm2.
Perimeter of the rectangle = 2 × (l + w)
= 2 × (11.2 + 5. 6)
= 2 × 16.8
= 33.6
So, perimeter of the rectangle is 33.6 cm.
Problem 8 :
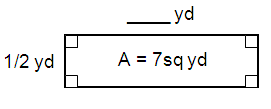
Solution :
By observing the figure,
Length = _____ yd
Width = 1/2 yd
area of the rectangle = 7 sq yd
Area of the rectangle = l × w
7 = l × 1/2
l = 14
So, length of the rectangle is 14 yd2.
Perimeter of the rectangle = 2 × (l + w)
= 2 × (14 + 1/2)
= 2 × (14/1 × 2/2 + 1/2)
= 2 × (28/2 + 1/2)
= 2 × (29/2)
= 58/2
So, perimeter of the rectangle is 29 yd.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling