PERCENTAGE INCREASE OR DECREASE

Problem 1 :

In a sale the price of a sofa is reduced from $2500 to $1840 what is the percentage decrease?

Solution :

The price of a sofa is reduced from $2500 to $1840.

Reduction amount = |2500 - 1840|

= 660

Percentage decrease = (660/2500) × 100%

= 26.4%

Problem 2 :

The population of Northern Ireland in 1911 was 1,256,561 in 2011 the population was 1,810, 863.

• Calculate the percentage increase.
• Give your answer correct to one decimal place.

Solution :

Population in 1911 = 1256561

Population in 2011 = 1810863

Difference = |1810863 - 1256561|

= 554302

Percentage increase= (554302/1256561) × 100%

= 44.1%

Problem 3 :

In 2000 the price of a house was $72,600. By 2010 the price of the house had increased to $ 125,598. Find the percentage increase in the price of the house from 2000 to 2010.

Solution :

2000 the price of a house = $72,600

2010 the price of a house = $125598

Difference = |125598 - 72600|

= 52998

Percentage increase= (52998/72600) × 100%

= 73%

Problem 4 :

A website had 140,000 views in March. It had 198,800 views in April. Work out the percentage increase in views.

Solution :

Views in March = 140000

Views in April = 198800

Difference = |198800 - 140000|

= 58800

Percentage increase = (58800/140000) × 100%

= 42%

So, 42%  Percentage increase in views.

Problem 5 :

In a sale the price of microwave decreases from $50 to $39. Work out the percentage decrease in price.

Solution :

The price of microwave decreases from $50 to $39.

Decrease amount = |50 – 39|

= 11

Difference = (11/50) × 100%

= 22%

So, the percentage decrease in price = 22%.

Problem 6 :

An empty bucket weight 800 g. The weight of the bucket increases to 2.1 kg when filled with water.

Calculate the percentage increase in the weight of the bucket. Give your answer to two significant figures.

Solution :

Weight of empty bucket = 800 g

Converting into kg.

= 0.8 kg

When it was with water = 2.1 kg

= |2.1 - 0.8|

= 1.3

The percentage increase in the weight of the bucket

= (1.3/0.8) × 100%

= 1.625%

Problem 7 :

Orla weighed 3.77 kg when she was born. On Orla’s second birthday she weighed 12.8 kg. Calculate the percentage increase in her weight.

Solution :

Weight of her  = 3.77 kg

Weight of her on second birthday = 12.8 kg

Difference in weight = |3.77 - 12.8|

= 9.03

Percentage increase = (9.03/3.77) × 100%

= 239.52%

So, the percentage increase in her weight is 239.52%

Problem 8 :

Rebecca and Jennifer take part in a training camp to improve their performance at the javelin.

The table below shows Rebecca’s and Jennifer’s best javelin throw before and after the training camp.

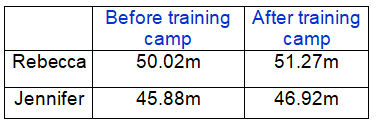
Which athlete had the biggest percentage improvement?

You must show your method.

Solution :

Rebecca :

Before training camp = 50.02m

After training camp = 51.27m

Training camp = |50.02 – 51.27|

= 1.25

Percentage increase = (1.25/50.02) × 100%

= 2.499%

Jennifer :

Before training camp = 45.88m

After training camp = 46.92m

Training camp = |45.88 – 46.92|

= 1.04

Percentage increase = (1.04/45.88) × 100%

= 2.2668%

So, Rebecca has improved.

Problem 9 :

The table shows the number of hours you spent online last weekend. What is the percent of change in your online time from Saturday to Sunday?

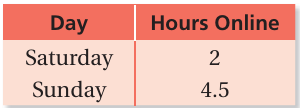
Solution :

Number of hours spent online on Saturday = 2

Number of hours spent online on Sunday = 4.5

Percentage change = (4.5 - 2)/2 x 100%

= (2.5/2)x100%

= 1.25x100%

 = 125%

125% increase on Sunday.

Problem 10 :

After a decrease of 35%, a number becomes 520. Find the original number.

Solution :

Let x be the original number.

35% decrease, then 65% of x = 520

0.65x = 520

x = 520/0.65

x = 800

So, the original number is 800.

Problem 11 :

By selling a motor cycle for $230 a dealer gains 15% . Find its cost price.

Solution :

Cost of motor cycle = $230

Gain of 15%.

Cost price after fain of 15% = 115% of 230

= 1.15(230)

= 264.5

So, the cost price is $265.

Problem 12 :

A batsman scored 110 runs which included 3 boundaries and 8 sixes. What per cent of his total score did he make by running between the wickets ?

Solution :

Total runs = 110

Number of boundaries = 4

Runs via boundaries = 3(4) ==> 12

Number of sixes = 8

Runs via sixes = 6(8) ==> 48

Number of runs between wickets = 110 - (12 + 48)

= 110 - 60

= 50

Percentage of total score = (50/110) x 100%

= 45.45%

Approximately 45%.

Problem 13 :

Anil sold two washing machines at $120 each. On one he gains 25% and on the other he loses 25%. How much does he gain or lose in the whole transaction.

Solution :

Cost price of each washing machine = $120

Gain of 25% = 125% of 120

= 1.25(120)

= $150

Loss of 25% = 75% of 120

= 0.75(120)

= $90

Cost price of two washing machines = 2(120)

= $240

Selling price of two washing machines = 150 + 90

= $240