PARALLEL AND PERPENDICULAR LINES SAT QUESTIONS

Problem 1 :

In the xy plane, the lines

y = mx - 7 are 2x + 3y = 6

are parallel. What is the value of m ?

Solution

Problem 2 :

A line passes through the points (-1, 2) and (5, b) and is parallel to the graph of the equation 4x - 2y = 13. What is the value of b ?                Solution

Problem 3 :

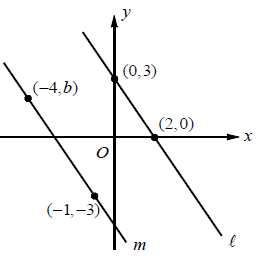
In the xy - plane above, line l is parallel to line m. What is the value of b?

Solution

Problem 4 :

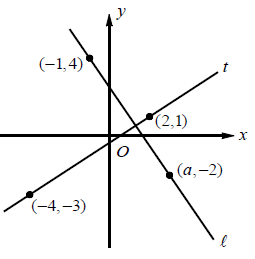
In the xy-plane above, if line l is perpendicular to line t, what is the value of a? 

Solution

Problem 5 :

kx - 3y = 4

4x - 5y = 7

In the system of equation above, k is constant and x and y are variables. For what value of k will the system of equation have no soltuion ?

a)  12/5    b)  16/7     c)  -16/7    d)  -12/5

Solution

Problem 6 :

(3/2)y - (1/4)x = 2/3 - (3/2)y

(1/2)x + 3/2 = py + (9/2)

In the given system of equation p is constant. If the system has no solution. What is the value of p ?

Solution

Problem 1 :

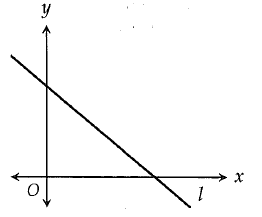
The graph of the line l is shown in the xy plane above. The equation of line n (not shown) is y = mx + b, where m and b are constants. If line l is perpendicular to the line n, which of the following must be true ?

(a)  m < 0     (b) m > 0       (c)  b < 0     (d) b > 0

Solution

Problem 2 :

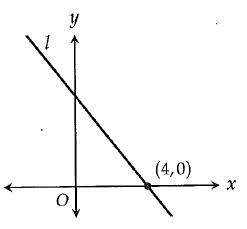
In the xy plane above, line l has slope -5/4. What is the area of the triangle bounded by the line l, the x-axis and the y-axis ?

(a)  5    (b)  8     (c)  10     (d)  16

Solution

Problem 3 :

In the xy plane, the line with the equation 3x + 4y = 6 is perpendicular to the line with the equation y = mx + b, where m and b are constants. What is the value of m ?

(a)  4/3    (b)  -4/3     (c)  3/4     (d)  -3/4

Solution

Problem 4 :

If m and b are real numbers and m > 0 and b > 0 then the line whose equation is y = mx + b cannot contain which of the following points ?

(a)  (0, 1)     (b)  (1, 1)      (C)  (-1, 1)      (d) (0, -1)

Solution

Problem 5 :

In which of the following figures is the slope of the line shown closest to -1/2 ?

Solution

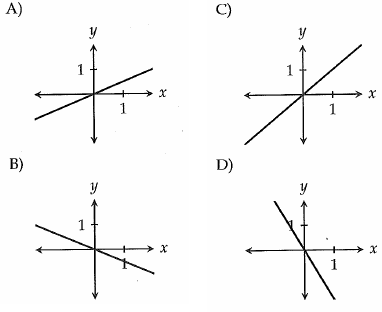
Problem 6 :

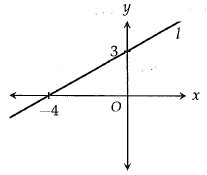
The graph of the line l is shown in the xy plane above. The y-intercept of the line l is 3 and the x-intercept is -4. If the line m is perpendicular to line l, what is the slope of the line m ?

(a)  -4/3     (b)  -3/4      (C)  -1/2      (d) 3/4

Solution

Problem 7 :

In the xy-plane, line l passes through (0, 0) and is perpendicular to the line 3x + y = c, where c is a constant. If two lines intersect at the point (k, k - 4), what is the value of k ?

(a)  4     (b)  6      (C)  8      (d) 10

Solution

Problem 1 :

A, B and C have coordinates (2, 9), (10, −7) and (6, k) respectively. AB is perpendicular to AC.

Solution

Problem 2 :

Line A passes through the points (3, 6) and (5, -2) Line B passes through the points (2, 5) and (8, k) Line A and Line B are parallel. Find the value of k.

Solution

Problem 3 :

Line A passes through the points (-3, -1) and (-1, 9) Line B passes through the points (-2, 1) and (k, 4) Line A and Line B are perpendicular. Find the value of k.

Solution

Problem 4 :

The line through (−1, k) and (−7, −2) is parallel to the line y = x + 1. Find a value for k based on the given description.

Solution

Problem 5 :

The line through (k, 2) and (7, 0) is perpendicular to the line y = x − (28/5). Find a value for k based on the given description.

Solution

Problem 6 :

If A (1, 3), B (–1, 2), C (2, 5) and D (x, 4) are the vertices of parallelogram ABCD then the value of x is

(a) 3        (b) 4     (c) 0            (d) 3/2

Solution

Problem 7 :

A straight line is perpendicular to the straight line passing through (2, 8) and (6, 15) and passes through (0, 9) and (x, 17). Find the value of x.

Solution