ORDER THE SIDES OF THE TRIANGLE FROM SHORTEST TO LONGEST WORKSHEET

The following triangles are not drawn to scale.

(i) Find the missing angle

(ii)  State the longest side of each triangle.

Problem 1 :

Solution

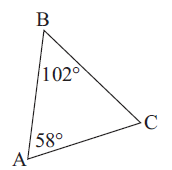
Problem 2 :

Solution

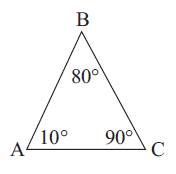
Problem 3 :

List the sides of each triangle in order from shortest to longest.

Solution

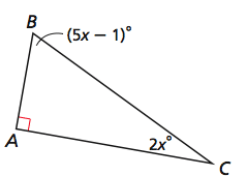
Problem 4 :

List the sides of each triangle in order from shortest to longest.

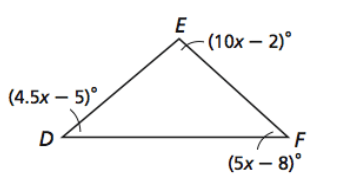
Problem 5 :

Determine the Longest side of ∆MNO, where m∠M = 56, m∠N = 108, and m∠O = 16

Solution

Problem 6 :

List the sides in order from shortest to longest in ∆ XYZ :

with m∠X = 50, m∠Y = 5x + 10 and m∠Z = 5x.

Solution

Problem 7 :

Which is the longest and which is the smallest.

Solution

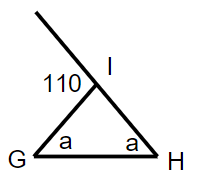
Problem 8 :

Which is the longest and which is the smallest.

Solution

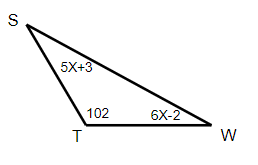
Problem 9 :

Find the longest side.

Solution

Problem 10 :

In the diagram of quadrilateral NAVY below, m∠YNA = 30°, m∠YAN = 38°, m∠AVY = 94°, and m∠VAY=46°

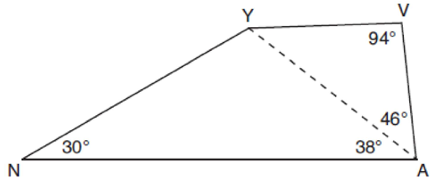
Which segment has the shortest length?

a) AY      b) NY       c) VA      d) VY

Solution

Problem 11 :

In triangle ABC, m∠B < m∠A  < m∠C. Which statement is false ?

a)  AC > BC     b)  BC > AC     c)  AC < AB    d) BC < AB

Solution

Problem 1 :

In ∆ABC, m∠A = 90, m∠B = 55 and m∠C = 35.

a) List the sides in order from smallest to largest.

b) Classify the triangle by its sides.

Solution

Problem 2 :

In ∆ABC, m∠B = 140 and m∠C = 20.

a) List the sides in order from smallest to largest.

b) Classify the triangle by its angles.

Solution

Problem 3 :

In ∆PQR, PQ = 8, QR = 12, and RP = 13.

a) List the angles in order from smallest to largest.

b) Classify the triangle by its sides.

Solution

Problem 4 :

In ∆ABC, measure of ∠ACB = 70˚ and the measure of ∠ABC = 65˚

a) List the sides in order from smallest to largest.

b) Classify the triangle by its angles.

Solution

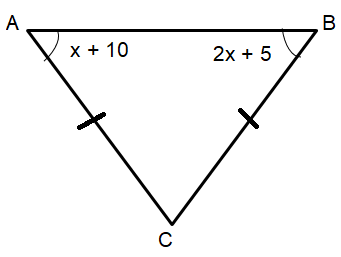
Problem 5 :

The triangle above is isosceles and b > a. Which of the following must be FALSE ?

a)  AB = BC     b)  AB = AC     c)  AC = BC     d) a = c

Solution

Problem 6 :

As shown in the diagram below of ABC, BC is extended through D, m∠A = 70, and m∠ACD = 115

Which statement is true?

a) AC > AB      b) AB > BC      c) BC < AC      d) AC < AB

Solution

Problem 7 :

In ABC, m∠A = 60, m∠B = 80, and m∠C = 40. Which inequality is true?

a) AB > BC     b) AC > BC      c) AC < BA     d) BC < BA

Solution

Problem 8 :

In triangle ABC, m∠B < m∠A < m∠C. Which statement is false?

a) AC > BC     b) BC > AC     c) AC < AB      d) BC < AB

Solution

Problem 9 :

∆XYZ is an isosceles triangle with equal angles 1 and 2 shown. Find :

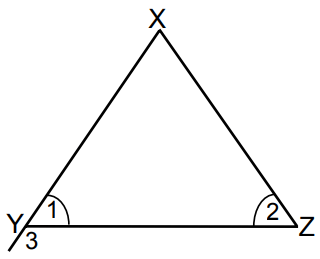
a) the size of ∠2 if ∠X = 56°.

b) the size of ∠3.

c) the longest side of ∆XYZ.

Solution

Problem 10 :

∆RST is isosceles with angles S and T equal. ∠R = 40°.

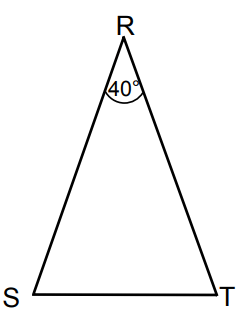
a) What is the size of ∠S?

b) What is the shortest side of ∆RST?

Solution

1)

a) Order of the sides from smallest to largest:

AB < AC < BC

b) All three sides are different. So it is scalene triangle.

2)

In ∆ABC, the longest side is AC and the remaining two sides BC and AB are equal in length.

b)   In the triangle, two of the angles are congruent. So, it is isosceles obtuse triangle.

3)

Order of the angles from smallest to largest:

 ∠R < ∠P < ∠Q

b)  All three sides are different. So it is scalene triangle.

4)

a) Order of the sides from smallest to largest:

BC < AC < AB

b)

i. All the three angles are different.

ii. Each of the three angles is less than 90˚.

So, the triangle is a scalene and acute triangle.

5) option c is FALSE.

6) AC < AB is true.

7)  AC > BC is true.

8) AC is greater than BC.

9) a) ∠1 = 62 = ∠2

b) ∠3 = 118

c) c)  XY and XZ will have the same measure.

10) In the triangle above ∠R is smallest, then ST is the smallest side.