ORDER OF OPERATIONS WITH FRACTIONS AND DECIMALS

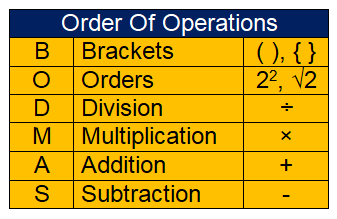
BODMAS is the rule that can be used to simplify or evaluate complicated numerical expressions with more than one  operation.

Example 1 :

1  1/4 x 6 - (1/2)²

Solution :

= 1  1/4 x 6 - (1/2)²

Converting the mixed fraction to improper, we get

Example 2 :

1.55 + (0.5)² - 4.9 ÷ 7

Solution :

Example 3 :

1  2/7 x (2/3)² - (6/7²) ÷ (1/7)

Solution :

= 1  2/7 x (2/3)² - (6/7²) ÷ (1/7)

Converting the improper fraction to mixed fraction, we get

= (9/7) x (2/3)² - (6/7²) ÷ (1/7)

Using exponents, we get

= (9/7) x (4/9) - (6/49) ÷ (1/7)

Multiplying the first two fractions, we get

= 4/7 - (6/49) ÷ (1/7)

Dividing 6/49 by 1/7, we get

= 4/7 - (6/7)

= (4 - 6)/7

= -2/7

Example 4 :

(2.4)² + 5.6 x 1.6

Solution :

= (2.4)² + 5.6 x 1.6

= 5.76 + 5.6 x 1.6

= 5.76 + 8.96

= 14.72

Example 5 :

(1/2)² x (4/5) - (6/5)

Solution :

= (1/2)² x (4/5) - (6/5)

By using exponent, we get

= (1/4) x (4/5) - (6/5)

= (1/5) - (6/5)

= (1-6)/5

= -5/5

= -1

Example 6 :

18.14 + (0.5)³ ÷ 2.5 - 21.13

Solution :

Example 7 :

1.9 - 3² x 0.3 + 16.1

Solution :

Example 8 :

(1/3)² ÷ 1/9 + 2/3 -15/2 x 2/5

Solution :

= (1/3)² ÷ 1/9 + 2/3 -15/2 x 2/5

= (1/9) ÷ 1/9 + 2/3 -15/2 x 2/5

= 1 + 2/3 -15/2 x 2/5

= 1 + 2/3 - 3

= (3 + 2 - 9)/3

= -4/3

Example 9 :

2.16 ÷ 6² - 13.06 + 1.2 x 0.5

Solution :

= 2.16 ÷ 6² - 13.06 + 1.2 x 0.5

= 2.16 ÷ 36 - 13.06 + 1.2 x 0.5

= 0.06 - 13.06 + 1.2 x 0.5

= 0.06 - 13.06 + 0.6

= -13 + 0.6

= -12.4

Example 10 :

(2/3) ÷ (2/3) x 2² + 1 1/2

Solution :

= (2/3) ÷ (2/3) x 2² + 1 1/2

= (2/3) ÷ (2/3) x 2² + 1 1/2

= 1 x 4 + 1 1/2

= 4 + 3/2

= (8 + 3)/2

= 11/2

Example 11 :

Which expression is not equivalent to 2/3 ?

a)  1/4 + 1/3 ÷ (4/5)       b) 13/30 + 1/5 ÷ (6/7)

c)  5/6 - 1/8 ÷ 1/2           d)  13/18 - 1/26 ÷ 9/13

Solution :

Option a :

= 1/4 + 1/3 ÷ (4/5)

= (3 + 4)/12 ÷ (4/5)

= 7/12 ÷ (4/5)

= 7/12 x (5/4)

= 35/48

So, option a is not correct.

Option b :

= 13/30 + 1/5 ÷ (6/7)

= 13/30 + 1/5 x (7/6)

= 13/30 + 7/30

= (13 + 7)/30

= 20/30

= 2/3

Example 12 :

which of the following expressions is equivalent to a perfect square ?

a)  3 + 2² x 7       b)  (80 + 4) ÷ 4      c)  34 + 18 ÷ 3²

d)  3² + 6 x 5 ÷ 3

Solution :

Option a :

= 3 + 2² x 7

= 3 + 4 x 7

= 3 + 28

= 31

31 is not a perfect square. So, option a is not correct.

b)

= (80 + 4) ÷ 4

= 84 ÷ 4

= 21

21 is not a perfect square. So, option b is not correct.

c) 

= 34 + 18 ÷ 3²

= 34 + 18 ÷ 9

= 34 + 2

= 36

36 is a perfect square, then option c is correct.

d)  3² + 6 x 5 ÷ 3

Example 13 :

A motocross rider is in the air for 2.5 seconds. Your camera can take a picture every 0.125 second. Your friend’s camera can take a picture every 0.15 second.

a. How many times faster is your camera than your friend’s camera?

b. How many more pictures can you take while the rider is in the air?

Solution :

a)  Number of times faster = 0.15/0.125

Multiplying both numerator and denominator by 1000, we get

= 150/125

= 30/25

= 6/5

= 1.2

Your camera is 1.2 times faster.

b) Number of pictures made by your camera = 2.5/0.125

= 20 pictures

Number of piuctures made by you'r friend camera = 2.5/0.15

= 250/15

= 50/3

= 16.6

Approximately 16 pictures

Example 14 :

You spend 2 1/2 hours online. You spend 1/5 of that time writing a blog. How long do you spend writing your blog?

Solution :

Time spending to write your blog = 1/5 of 2  1/2

= 1/5 x 5/2

= 1/2

Time spend to write your blog is 1/2 hours.

Example 15 :

To approximate the number of bees in a hive, multiply the number of bees that leave the hive in one minute by 3 and divide by 0.014. You count 25 bees leaving a hive in one minute. How many bees are in the hive?

Solution :

= 25 x 3 ÷ 0.014

= 75 ÷ 0.014

= 75/0.014

= 75000/14

= 5357.1

So, approximately 5357 bees.