ORDER OF OPERATIONS USING
BODMAS 

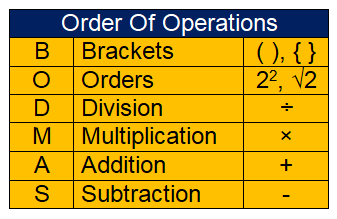
Note :

In some expressions, if there is multiplication and division, we have to do the operations one by one in the order from left to right.

Example 1 :

4 × 6 ÷ 2 - 8² + 15

Solution :

Example 2 :

4³ ÷ 8 × 2 - 7² + 1

Solution :

Example 3 :

10² - 8 × 8

Solution :

Example 4 :

22 + 45 ÷ 5 × 3²

Solution :

Example 5 :

96 ÷ 4² - 9² + 1

Solution :

Example 6 :

48 ÷ 2⁴ - 5

Solution :

Example 7 :

8 - 2² + 4 × 64 ÷ 4² 

Solution :

Example 8 :

15 × 3 - 1 + 9² ÷ 27

Solution :

Example 9 :

11 + 6² × 1

Solution :

Example 10 :

6² + 4 - 18 ÷ 6

Solution :

Example 11 :

3/4 % of 280 - 1/4 % of 800

Solution :

= 3/4 % of 280 - 1/4 % of 800

Simplifying the first term :

= (3/4) ⋅ 1/100 ⋅ 280

= (3/400) ⋅ 280

= (3 ⋅ 280) / 400

Simplifying the second term :

= (1/4) ⋅ 1/100 ⋅ 800

= (1/400) ⋅ 800

= (1 ⋅ 800) / 400

Subtracting these two results,

= (3 ⋅ 280) / 400 - (1 ⋅ 800) / 400

= [(3 ⋅ 280) - (1 ⋅ 800)] / 400

= (840 - 800)/400

= 40/400

= 1/10

= 0.1

Example 12 :

(1/4) x 20 - 4

Solution :

= (1/4) x 20 - 4

= (20/4) - 4

= 5 - 4

= 1

Example 13 :

9² - 8(6 + 2)

Solution :

= 9² - 8(6 + 2)

= 81 - 8(8)

= 81 - 64

= 17

Example 14 :

You have $9, one of your friends has $10, and two of your other friends each have $13. You combine your money to buy arcade tokens. You use a coupon to buy 8 tokens for $1. The cost of the remaining tokens is four for $1. You and your friends share the tokens evenly. How many tokens does each person get?

Solution :

Amount i have = $9

Amount my friend has = $10

Amount that my two friends have = 13

Total money that i have, my friend and my two friends have 

= 9 + 10 + 2(13)

= 9 + 10 + 26

= 45

For the first $1 there are 8 token

And after that cost of 4 tokens is $1,

Total tokens = 8×1 + 4×(45 - 1)

Total tokens = 8 + 176

Total tokens = 184

Now, Distribution among the fours,

= 184 / 4

= 46 tokens

Example 15 :

10 − 8(13 + 7) ÷ 4²

Solution :

= 10 − 8(13 + 7) ÷ 4²

4² = 4 x 4 ==> 16

= 10 - 8(20) ÷ 16

= 10 - 160 ÷ 16

Dividing 160 by 16, we get

= 10 - 10

= 0

Example 16 :

You borrow bookcases like the one shown to display 943 books at a book sale. You plan to put 22 books on each shelf. No books will be on top of the bookcases.

a. How many bookcases must you borrow to display all the books?

b. You fill the shelves of each bookcase in order, starting with the top shelf. How many books are on the third shelf of the last bookcase?

Solution :

Total number of books = 943

Total number of shelves = 5

Number of books places in each shelf = 22

a) Number of book cases = 943/22

= 42.8

= 43

Approximately 43 book cases are needed.

b)  42 x 5 = 210

Now, we calculate how many books can fit in these 210 shelves: 

210 x 22 = 4620

Since we only have 943 books, we will not fill all the shelves.

To find the number of books in the last bookcase, we calculate how many books are left after filling the first 42 bookcases. The total number of books that can fit in 42 bookcases is 924 (42 bookcases x 22 books per shelf). Therefore, the number of books remaining for the last bookcase is:$$

Since the last bookcase is the 43rd one, and we are filling the shelves starting from the top, the third shelf of the last bookcase will contain 19 books.

943 - 924 = 19