OPERATIONS WITH SCIENTIFIC NOTATION

Problem 1 :

(1.2 × 10⁵) + (5.35 × 10⁶)

Solution :

= (1.2 × 10⁵) + (5.35 × 10⁶)

In order to simplify further, we have to make exponents same.

1.2 × 10⁵ = 0.12 × 10¹ × 10⁵

By combining the powers using a^m ⋅ aⁿ = a^{m + n} , we get

= 0.12 × 10^{(1+ 5)}

= 0.12 × 10⁶

1.2 × 10⁵ = 0.12 × 10⁶  ------(1)

5.35 × 10⁶ = 5.35 × 10⁶   ------(2)

(1) + (2)

= (0.12 × 10⁶) + (5.35 × 10⁶)

= (0.12 + 5.35) × 10⁶

= 5.47 × 10⁶

Problem 2 :

(3.67 × 10²) - (1.6 × 10¹)

Solution :

(3.67 × 10²) - (1.6 × 10¹)

In order to simplify further, we have to make exponents same.

1.6 × 10¹ = 0.16 × 10¹ × 10¹

By combining the powers using a^m ⋅ aⁿ = a^{m + n} , we get

= 0.16 × 10^{(1+ 1)}

= 0.16 × 10² 

3.67 × 10² = 3.67 × 10² ------(1)

1.6 × 10¹ = 0.16 × 10²  ------(2)

(1) - (2)

= (3.67 × 10²) - (0.16 × 10²)

= (3.67 - 0.16) × 10²

= 3.51 × 10²

Problem 3 :

(4.3 × 10⁸) × (2.0 × 10⁶)

Solution :

= (4.3 × 10⁸) × (2.0 × 10⁶)

To simplify further, we have to make exponents same.

2.0 × 10⁶ = 0.02 × 10² × 10⁶

= 0.02 × 10^{(2 + 6)}

= 0.02 × 10⁸

= (4.3 × 10⁸) × (0.02 × 10⁸)

= (4.3 × 0.02) × 10⁸

= 0.086 × 10⁸

= 8.6 × 10^8-2

= 8.6 × 10⁶

Problem 4 :

(7.8 × 10³) / (1.2 × 10⁴)

Solution :

= (7.8 × 10³) / (1.2 × 10⁴)

To simplify further, we have to make exponents same.

7.8 × 10³ = 0.78 × 10¹ × 10³

= 0.78 × 10^{(1 + 3)}

= 0.78 × 10⁴

(7.8 × 10³) / (1.2 × 10⁴) = (0.78 × 10⁴)/(1.2 × 10⁴)

= (0.78/1.2) × 10^{4 + 4}

= 0.65 × 10⁸

= 6.5 × 10^8-1

= 6.5 × 10⁷

Problem 5 :

Evaluate the expression using two different methods. Write your answer in scientific notation. 

a)  (2.74 × 10⁷) + (5.6 × 10⁷)

b)  (8.3 × 10⁶) x (3.4 × 10⁵)

c)  (5.1 × 10⁵) × (9.7 × 10⁵)

d)  (4.5 × 10⁴) × (6.2 × 10³)

Solution :

a)  (2.74 × 10⁷) + (5.6 × 10⁷)

2.74 × 10⁷ = 27400000

5.6 × 10⁷ = 56000000

= 27400000 + 56000000

= 83400000

b)  (8.3 × 10⁶) x (3.4 × 10⁵)

= 8.3 x 3.4 × 10⁶  x 10⁵

= 8.3 x 3.4 × 10⁶⁺⁵

= 28.22 x 10¹¹

Since we have power 11, we have to move the decimal 11 digits. We have two digits after the decimal. Then we have to write 9 more zeros.

= 2822000000000

c)  (5.1 × 10⁵) × (9.7 × 10⁵)

= 5.1 x 9.7 × 10⁵  x 10⁵

= 5.1 x 9.7 × 10⁵⁺⁵

= 49.47 x 10¹⁰

Since we have power 10, we have to move the decimal 10 digits. We have two digits after the decimal. Then we have to write 8 more zeros.

= 494700000000

d)  (4.5 × 10⁴) × (6.2 × 10³)

= 4.5 x 6.2 × 10⁴ × 10³

= 27.9 × 10⁴⁺³

= 27.9 × 10⁷

= 279000000

Problem 6 :

How many times greater is the thickness of a dime than the thickness of a dollar bill?

Solution :

Thickness of coin = 0.135 cm

Thickness of note = 1.0922 x 10^-2 cm

=  0.135 / 1.0922 x 10^-2 

= 0.1236 x 10² 

= 12.36

So, the thinck ness of dime coin is 12 times of dollar bill.

Problem 7 :

Evaluate the expression. Write your answer in scientific notation.

a) 5,200,000 × ( 8.3 × 10²) − (3.1 × 10⁸)

b) (9 × 10⁻³) + (2.4 × 10^-5) ÷ 0.0012

Solution :

a) 5,200,000 × ( 8.3 × 10²) − (3.1 × 10⁸)

= 5.2 x 10⁶ x ( 8.3 × 10²) − (3.1 × 10⁸)

= 5.2 x 8.3 x 10⁶ x 10² − (3.1 × 10⁸)

= 43.16 x 10⁶⁺² - (3.1 × 10⁸)

= 43.16 x 10⁸ - (3.1 × 10⁸)

= 4316000000 - 310000000

= 4006000000

= 4.006 x 10⁹

b) (9 × 10⁻³) + (2.4 × 10^-5) ÷ 0.0012

= 0.009 + (2.4 × 10^-5) ÷ 1.2 x 10^-3

= 0.009 + (2.4 / 1.2) × 10^-5/ 10^-3

= 0.009 + 2 × 10^-5+3

= 0.009 + 2 × 10^-2

= 0.009 + 0.002

= 0.011

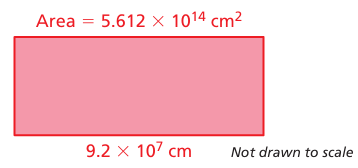
Problem 8 :

Find the perimeter of the rectangle.

Solution :

Area = 5.612 × 10¹⁴ cm²

Length = 9.2 × 10⁷

Width = 5.612 × 10¹⁴ / 9.2 × 10⁷

= 5.612/9.2 × 10¹⁴ x 10^-7

= 5.612/9.2 × 10¹⁴ x 10^-7

= 0.61 × 10^14-7

width = 0.61 × 10⁷

Perimeter = 2(length + width)

= 2(9.2 × 10⁷ + 0.61 × 10⁷)

= 2(9.81 × 10⁷)

= 19.62 × 10⁷

= 1.962 × 10^7-1

= 1.962 × 10⁶