NAME THE PROPERTY USED IN EACH STEP
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Addition Property :
Adding the same quantity on both sides of the equal sign will never change the given question.
For example,
If AB = CD
Adding 2 on both sides, we get
AB + 2 = CD + 2
Subtraction Property :
Subtracting the same quantity on both sides of the equal sign will never change the given question.
For example,
If AB = CD
Subtracting 2 on both sides, we get
AB - 2 = CD - 2
Multiplication and division Property :
Multiplying and dividing by same quantity on both sides will never change the original question.
For example,
If AB = CD ----(1)
Multiplying by 2 on both sides, we get
2AB = 2CD
From (1)
Dividing by 2 on both sides, we get
AB/2 = CD/2
Reflexive property :
If same quantities on both side of the equal sign, then they will be equal.
That is,
a = a
Substitution property :
Given that x + y = 7, find x when y = 1
Here in the given question, instead of the variable y we have to apply the its value 1.
x + y = 7
x + 1 = 7
Subtracting 1 on both sides, we get
x + 1 - 1 = 7 - 1
x = 6
Distributive Property :
If a (b + c)
then,
a (b + c) = ab + ac
Problem 1 :
Fill in the reason that justifies each step.
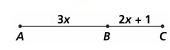
Given: AC = 36
AB + BC = AC ______
3x + 2x + 1 = 36 ______
5x + 1 = 36 ______
5x = 35 ______
x = 7 ____
Solution:
Given:
AB + BC = AC
The length of AB is 3x and length of BC is 2x + 1
Substitution Property:
Using substitution property, applying the values of AB and BC.
3x + 2x + 1 = 36
Addition Property:
Using addition property adding the like terms,
5x + 1 = 36
Subtraction Property:
Using subtracting property, subtracting 1 on both sides,
5x = 35
Division Property:
Using division property, divide by 5 on both sides,
x = 7
So, the value of x is 7.
Problem 2 :
Solve the equation and state the reason for each step.
5(2x - 1) = 9x + 4
Solution:
Given:
5(2x - 1) = 9x + 4
Distributive Property:
Distribute 5 to 2x and 1.
10x - 5 = 9x + 4
Subtraction Property:
Subtract 9x from each side of the equation.
x - 5 = 4
Addition Property:
Add 5 to each side.
x = 9
Problem 3 :
In the diagram at the right, m∠WPY = m∠XPZ. Complete the argument to show that m∠WPX = m∠YPZ.
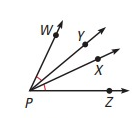
|
m∠WPY = m∠XPZ m∠WPX = m∠WPY + m∠YPX m∠YPZ = m∠YPX + m∠XPZ m∠WPY + m∠YPX = m∠YPX + m∠XPZ m∠WPX = m∠YPZ |
Given ? ? ? ? |
Solution :
Step 1 :
m∠WPX = m∠WPY + m∠YPX ---(1)
Substituting the value of m∠WPX,
Here m∠WPX is the sum of m∠WPY and m∠YPX
Step 2 :
m∠YPZ = m∠YPX + m∠XPZ ---(2)
Substituting the value of m∠YPZ,
Here ∠YPZ is the sum of m∠YPX and m∠XPZ
Step 3 :
With the given
m∠WPY = m∠XPZ
Using addition property, adding m∠YPX on both sides.
m∠WPY + m∠YPX = m∠YPX + m∠XPZ
Step 4 :
Using reflexive property, from step 1 and step 2
m∠WPX = m∠YPZ
Problem 4 :
Which properties are missing in the steps to solve the equation:
76 = 5x - 15 + 2x
Solution:
|
76 = 5x - 15 + 2x 76 = 5x + 2x - 15 76 = 7x - 15 91 = 7x x = 13 |
Original Equation Addition Property of Equality Addition Property of Equality Division Property of Equality Answer |
Problem 5 :
Fill in the missing properties and equation in the steps to solve the equation
5x + 3(x + 4) = 28?
Solution:
|
5x + 3(x + 4) = 28 5x + 3x + 12 = 28 8x + 12 = 28 8x = 16 x = 2 |
Original Equation Distributive Property of Equality Addition Property of Equality Subtraction Property of Equality Division Property of Equality |
Identify the property of equality that justifies each missing step or equation in each of the following tables.
Problem 6 :
Solution:
|
x + (x - 0.6) = 2 x + x - 0.6 = 2 2x - 0.6 = 2 2x = 2.6 x = 1.3 |
Original Equation Distributive Property of Equality Addition Property of Equality Subtraction property of equality Division Property of Equality |
Problem 7 :
Solution:
|
x + (4x + 32) = 12 5x + 32 = 12 5x = -20 x = -4 |
Original Equation Addition Property of Equality Subtraction Property of Equality Division Property of Equality |
Problem 8 :
Solution:
|
4(x - 6) = 40 x - 6 = 10 x = 16 |
Original Equation Division Property of Equality Addition Property of Equality |
Problem 9 :
Solution:
|
1.4 - 0.3x + 0.7x = 9.4 1.4 + 0.4x = 9.4 0.4x = 8 x = 20 |
Original Equation Addition Property of Equality Subtraction Property of Equality Division Property of Equality |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling