MULTIPLYING TWO BINOMIALS WITH RADICALS

Expand and simplify :

Problem 1 :

(1 + √2) (2 + √2)

Solution :

(1   + √2) (2 + √2)

= (1) (2 + √2) + (√2) (2 + √2)

= 2 + √2 + 2√2 + √2 ⋅ √2

= 2 + 3√2 + 2

= 4 + 3√2

Problem 2 :

(2 + √3) (3 + √3)

Solution :

(2 + √3) (3 + √3)

= 2 (3 + √3) + (√3) (3 + √3)

= 6 + 2√3 + 3√3 + √3 ⋅√3

= 6 + 5√3 + 3

= 9 + 5√3

Problem 3 :

(4 - √2) (3 + √2)

Solution :

(4 - √2) (3 + √2)

= 4(3 + √2) - √2(3 + √2)

= 12 + 4√2 - 3√2 - √2 ⋅√2

= 12 + √2 – 2

= 10 + √2 

Problem 4 :

(1 + √3) (1 - √3)

Solution :

(1 + √3) (1 - √3)

= (1)(1 - √3) + (√3)(1 - √3)

= 1 - √3 + √3 - √3 ⋅√3

= 1 - 3

= -2

Problem 5 :

(√5 + 2) (√5 - 3)

Solution :

(√5 + 2) (√5 - 3)

= (√5)(√5 - 3) + 2 (√5 - 3)

= √5 ⋅√5 - 3√5 + 2√5 – 6

= 5 - √5 – 6

= -1 - √5

Problem 6 :

(6 - √3) (2 + √3)

Solution :

(6 - √3) (2 + √3)

= 6(2 + √3) - √3(2 + √3)

= 12 + 6√3 - 2√3 - √3 ⋅√3

= 12 + 4√3 – 3

= 9 + 4√3 

Problem 7 :

(4 - 3√3) (2 - √3)

Solution :

(4 - 3√3) (2 - √3)

= (4) (2 - √3) - (3√3) (2 - √3)

= 8 - 4√3 - 6√3 + 3(√3 ⋅ √3)

= 8 - 10√3 + 9

= 17 - 10√3

Problem 8 :

(-1 + 2√2) (2 - √2)

Solution :

(-1 + 2√2) (2 - √2)

= (-1)(2 - √2) + 2√2(2 - √2)

= -2 + √2 + 4√2 – 2(√2 ⋅ √2)

= -2 + 5√2 – 4

= -6 + 5√2 

Problem 9 :

4√3 (2√3 - 3√6)

Solution :

= 4√3 (2√3 - 3√6)

Distributing 4√3, we get

= 4√3(2√3) - 4√3(3√6)

= 8 √3√3 - 12√3√6

= 8(3) - 12√(3 x 6)

= 24 - 12√(3 x 3 x 2)

= 24 - (12 x 3)√2

= 24 - 36√2

Problem 10 :

(3√x - √y)²

Solution :

= (3√x - √y)²

Comparing with (a - b)² = a² - 2ab + b²

a = 3√x and b = √y

= (3√x)² - 2(3√x)(√y) + (√y)²

= 3² (√x)² - 6√x√y + y

= 9x - 6√xy + y

Problem 11 :

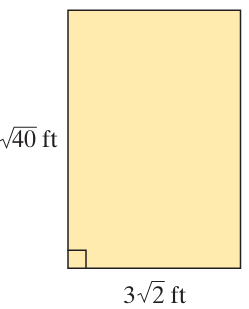
Solution :

Length = 3√2 ft and width = √40 ft

Area of rectangle = length x width

= 3√2(√40)

= 3(√2√40)

= 3√(2 x 2 x 2 x 5)

= 3 x 2 √10

= 6√10

So, area of rectangle is 6√10 square feet

Problem 12 :

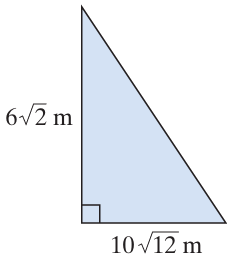
Solution :

Length = 10√12 m and height = 6√2 m

Area of triangle = (1/2) x base x height

= (1/2) x 10√12 x 6√2

= 5√12 x 6√2

= 5√(2 x 2 x 3) x 6√2

= (5 x 2)√3 x 6√2

= 10√3 x 6√2

= 60√(3 x 2)

= 60√6

So, area of triangle is 60√6 square meter.

Problem 13 :

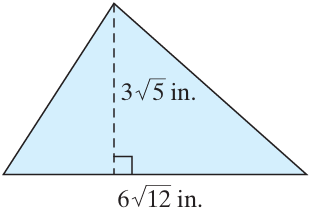
Solution :

Length = 6√12 m and height = 3√5 m

Area of triangle = (1/2) x base x height

= (1/2) x 6√12 x 3√5

= 3√12 x 3√2

= (3 x 3)√(2 x 2 x 3) x 3√2

= (3 x 3 x 2)√3 x 3√2

= 54√(3 x 2)

= 54√6

So, area of triangle is 54√6 square meter

Problem 14 :

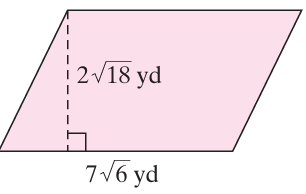
Solution :

Length = 7√6 yd and height = 2√18 yd

Area of parallelogram = base x height

= 7√6 x 2√18

= (7 x 2)√6√18

= 14√(6 x 6 x 3)

= (14 x 6)√3

= 84√3 square yards

So, area of parallelogram is 84√3 square yards.

Problem 15 :

Simplify 

-4 / (√3 - √5)

Solution :

= -4 / (√3 - √5)

Conjugate of √3 - √5 is √3 + √5

= -4(√3 + √5) / (√3 - √5) (√3 + √5)

= -4(√3 + √5) / (√3² - √5²)

= -4(√3 + √5) / (3 - 5)

= -4(√3 + √5) / (-2)

= 2(√3 + √5)

= 2√3 + 2√5

Problem 16 :

Simplify 

(√x + 2)/(3 - √x)

Solution :

= (√x + 2)/(3 - √x)

Conjugate of (3 - √x) is (3 + √x)

= (√x + 2)(3 + √x)/(3 - √x) (3 + √x)

Multiplying the numerator :

= (√x + 2) (3 + √x)

= 3√x + √x(√x) + 6 + 2√x

= 3√x + x + 6 + 2√x

= x + 6 + 5√x

Multiplying the denominator :

= (3 - √x) (3 + √x)

= 3² - (√x)²

= 9 - x

= (x + 6 + 5√x) / (9 - x)