MULTIPLYING POLYNOMIALS

Multiplying Monomial by a Polynomial

Find the product.

Problem 1 :

-8x⁴(-11x – 6)

Solution :

= -8x⁴(-11x – 6)

 = (-8x⁴)(-11x) + (-8x⁴)(-6)

= 88x⁵ + 48x⁴

Problem 2 :

3x²(10x⁷ + 6x²)

Solution :

= 3x²(10x⁷ + 6x²)

= 3x²(10x⁷) + 3x²(6x²)

= 30x⁹ + 18x⁴

Multiplying Binomials

Problem 3 :

(2x + 3)(x – 9)

Solution :

Given, (2x + 3)(x – 9)

Distribute.

= 2x(x – 9) + 3(x – 9)

Distribute again.

= 2x(x) + 2x(-9) + 3(x) – 3(9)

Multiply.

= 2x² – 18x + 3x – 27

Combine like terms.

= 2x² – 15x – 27

Problem 4 :

(x + 4y)(x + 4y)

Solution :

= (x + 4y)(x + 4y)

Using algebraic identity.

(a + b)² = a² + b² + 2ab

Given a = x, b = 4y

(x + 4y)² = (x)² + (4y)² + 2(x)(4y)

= x² + 16y² + 8xy

Problem 5 :

(9 + x)(4x – 12)

Solution :

Given, (9 + x)(4x – 12)

Distribute.

= 9(4x – 12) + x(4x – 12)

Distribute again.

= 9(4x) + 9(-12) + x(4x) + x(-12)

Multiply.

= 36x – 108 + 4x² – 12x

Combine like terms.

= 4x² + 24x – 108

Multiplying Binomial by Trinomial

Problem 6 :

(7y - 3)(49y² + 21y + 9)

Solution :

We can do this problems in two ways,

(i) Doing distribution

(ii) Algebraic identities

Method 1 :

= (7y - 3)(49y² + 21y + 9)

Distribute.

= 7y(49y² + 21y + 9) – 3(49y² + 21y + 9)

Distribute again.

= 7y(49y²) + 7y(21y) + 7y(9) + (-3)(49y²) + (-3)(21y) + (-3)(9)

Multiply.

= 343y³ + 147y² + 63y – 147y² – 63y – 27

Combine like terms.

= 343y³ - 27

Method 2 :

= (7y - 3)(49y² + 21y + 9)

= (7y - 3)((7y)² + 7y(3) + 3²)

It exactly matches with the algebraic identity, 

(a - b) (a² + ab + b²) = a³ - b³

= (7y)³ - 3³

= 343y³ - 27

Multiplying Trinomial by Trinomial

Problem 7 :

(3x² + 3x + 1) (x² + 2x + 3)

Solution :

Given, (3x² + 3x + 1) (x² + 2x + 3)

Distribute.

= 3x²(x² + 2x + 3) + 3x(x² + 2x + 3) + 1(x² + 2x + 3)

Distribute again.

= (3x²)(x²) + (3x²)(2x) + (3x²)(3) + 3x(x²) + 3x(2x) + 3x(3) + 1(x²) + 1(2x) + 1 (3)

Multiply.

= 3x⁴ + 6x³ + 9x² + 3x³ + 6x² + 9x + x² + 2x + 3

Combine like terms.

= 3x⁴ + 9x³ + 16x² + 11x + 3

Problem 8 :

3x(3x - 1)(2x + 9)

Solution :

= 3x(3x – 1)(2x + 9)

Distribute.

= (3x)[(3x)(2x + 9) + (-1)(2x + 9)]

Distribute again.

= (3x)[(3x)(2x) + 9(3x) + (-1)(2x) + (-1)(9)]

Multiply.

= (3x)[6x² + 27x – 2x – 9]

Combine like terms.

= (3x)[6x² + 25x – 9]

= 18x³ + 75x² – 27x

Using Algebraic Identities

Problem 9 :

(a - 10)(a + 10)

Solution :

= (a - 10)(a + 10)

Using algebraic identity.

(a + b)(a – b) = a² – b²

Given, a = a, b = 10

(a - 10)(a + 10) = (a)² – (10)²

= a² - 100

Problem 10 :

(7p + 10)(7p – 10)

Solution :

= (7p + 10)(7p – 10)

Using algebraic identity.

(a + b)(a – b) = a² – b²

Given a = 7p, b = 10

(7p + 10)(7p – 10) = (7p)² – (10)²

= 49p² - 100

Problem 11 :

(7m – 5w)(7m + 5w)

Solution :

= (7m – 5w)(7m + 5w)

Using algebraic identity.

(a + b)(a – b) = a² – b²

Given a = 7m, b = 5w

(7m – 5w)(7m + 5w) = (7m)² – (5w)²

= 49m² – 25w²

Problem 12 :

You are playing miniature golf on the hole shown.

a. Write a polynomial that represents the area of the golf hole.

b. Write a polynomial that represents the perimeter of the golf hole.

c. Find the perimeter of the golf hole when the area is 216 square feet.

Solution :

a.

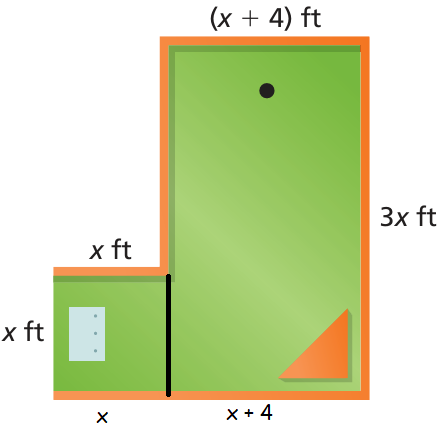
= Area of square + area of rectangle

= x(x) + (x + 4)3x

= x²+ 3x² + 12x

Arae of golf hole = (4x² + 12x) square feet

b. Perimeter of the golf hole = 4x + 2(x + 4 + 3x)

= 4x + 2(4x + 4)

= 4x + 8x + 8

= (12x + 8) ft

c. Given that, the area = 216 square feet

4x² + 12x = 216

4x² + 12x - 216 = 0

Dividing by 4, we get

x² + 3x - 54 = 0

x² + 9x - 6x - 54 = 0

x(x + 9) - 6(x + 9) = 0

(x - 6)(x + 9) = 0

x = -9 and x = 6

Perimeter of golf hole when x = 6

= 12(6) + 8

= 72 + 8

= 80 ft

Problem 13 :

A box in the shape of a rectangular prism has a volume of 96 cubic feet. The box has a length of (x + 8) feet, a width of x feet, and a height of (x − 2) feet. Find the dimensions of the box.

Solution :

Volume of rectangular prism = 96 cubic feet

length = x + 8, width = x and height = x - 2

(x + 8) x (x - 2) = 96

x(x² + 6x - 16) = 96

x³ + 6x² - 16x - 96 = 0

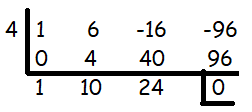
= (x - 4) (x² + 10x + 24)

= (x - 4)(x + 6)(x + 4)

(x - 4)(x + 6)(x + 4) = 0

x = 4, -6 and -4

Possible value of x is 4.

length = 12, width = 4 and height = 2