MULTIPLYING BINOMIALS USING DISTRIBUTIVE PROPERTY

Here we can see how we multiply binomials.

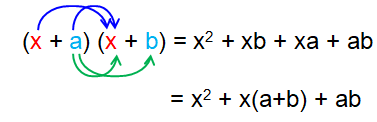
If two binomials are the same, we can use the algebraic identities instead of multiplying the binomials directly.

Problem 1 :

(x + 5) (x + 5)

Solution :

= (x + 5) (x + 5)

= x(x) + x(5) + 5(x) + 5(5)

= x² + 5x + 5x + 25

= x² + 10x + 25

Expand the following and collect like terms:

Problem 2 :

(x + 9) (x + 9)

Solution :

= (x + 9) (x + 9)

= x(x) + x(9) + 9(x) + 9(9)

= x² + 9x + 9x + 81

Combine the like terms.

= x² + 18x + 81 

Problem 3 :

(y - 2) (y - 2)

Solution :

= (y - 2) (y - 2)

= y(y) + y(-2) - 2(y) - 2(-2)

= y² - 2y – 2y + 4

Combine the like terms.

= y² - 4y + 4

Problem 4 :

(m - 3) (m - 3)

Solution :

= (m - 3) (m - 3)

= m(m) + m(-3) - 3(m) - 3(-3)

= m² - 3m – 3m + 9

Combine the like terms.

= m² - 6m + 9

Problem 5 :

(2m + 5) (2m + 5)

Solution :

= (2m + 5) (2m + 5)

= 2m(2m) + 2m(5) + 5(2m) + 5(5)

= 4m² + 10m + 10m + 25

Combine the like terms.

= 4m² + 20m + 25

Problem 6 :

(t + 10) (t + 10)

Solution :

= (t + 10) (t + 10)

= t(t) + t(10) + 10(t) + 10(10)

= t² + 10t + 10t + 100

Combine the like terms.

= t² + 20t + 100

Problem 7 :

 (y + 8)²

Solution :

(y + 8)² = (y + 8) (y + 8)

 = y(y) + y(8) + 8(y) + 8(8)

= y² + 8y + 8y + 64

Combine the like terms.

= y² + 16y + 64

Instead of multiplying the binomials directly, we can use algebraic identity (a + b)² = a² + 2ab + b²

(y + 8)² = y² + 2y(8) + 8²

= y² + 16y + 64

Problem 8 :

(t + 6)²

Solution :

(t + 6)² = (t + 6) (t + 6)

= t(t) + t(6) + 6(t) + 6(6)

= t² + 6t + 6t + 36

Combine the like terms.

= t² + 12t + 36