MULTIPLYING BINOMIALS BY ONE ANOTHER

Expand and simplify :

Example 1 :

(x + 4) (x + 3) (x + 2)

Solution :

By expanding first two factors, we get

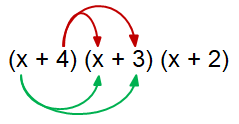
= [(x ∙ x) + (x ∙ 3) + (4 ∙ x) + (4 ∙ 3)] (x + 2)

= (x² + 3x + 4x + 12)(x + 2)

By combining like terms,

= (x² + 7x + 12) (x + 2)

By distributing x and 2, we get

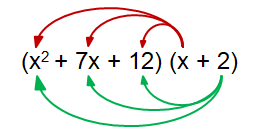
= (x² ∙ x) + (7x ∙ x) + (12 ∙ x) + (x² ∙ 2) + (7x ∙ 2) + (12 ∙ 2)

= x³ + 7x² + 12x + 2x² + 14x + 24

By combining like terms,

= x³ + 2x² + 7x² + 12x + 14x + 24

= x³ + 9x² + 26x + 24

Example 2 :

(x - 3)(x - 2)(x + 4)

Solution :

By expanding first two factors, we get

= [(x ∙ x) - (x ∙ 2) - (3 ∙ x) + (3 ∙ 2)] (x + 4)

= (x² - 2x - 3x + 6)(x + 4)

= (x² - 5x + 6)(x + 4)

By distributing x and 4, we get

= (x² ∙ x) + (-5x ∙ x) + (6 ∙ x) + (x² ∙ 4) + (-5x ∙ 4) + (6 ∙ 4)

= x³ - 5x² + 6x + 4x² - 20x + 24

By combining like terms,

= x³ - 5x² + 4x² + 6x - 20x + 24

= x³ - x² - 14x + 24

Example 3 :

(x - 3)(x - 2)(x - 5)

Solution :

By expanding first two factors, we get

= [(x ∙ x) - (x ∙ 2) - (3 ∙ x) + (3 ∙ 2)] (x - 5)

= (x² - 2x - 3x + 6) (x - 5)

= (x² - 5x + 6)(x - 5)

By distributing x and 2, we get

= (x² ∙ x) - (5x ∙ x) + (6 ∙ x) - (x² ∙ 5) + (5x ∙ 5) - (6 ∙ 5)

= x³ - 5x² + 6x - 5x² + 25x - 30

By combining like terms,

= x³ - 5x² - 5x² + 6x + 25x - 30

= x³ - 10x² + 31x - 30

Example 4 :

(2x - 3)(x + 3)(x - 1)

Solution :

By expanding first two factors, we get

= [2x(x) + 2x(3) - 3(x) - 3(3)] (x - 1)

= (2x² + 6x - 3x - 9) (x - 1)

= (2x² + 3x - 9) (x - 1)

= 2x²(x) - 2x²(1) + 3x(x) - 3x(1) - 9(x) + 9

= 2x³ - 2x² + 3x² - 3x - 9x + 9

= 2x³ + x² - 12x + 9

Example 5 :

(3x + 5)(x + 1)(x + 2)

Solution :

By expanding first two factors, we get

= [3x(x) + 3x(1) + 5(x) + 5(1)] (x + 2)

= (3x² + 3x + 5x + 5) (x + 2)

= (3x² + 8x + 5) (x + 2)

= 3x²(x) + 3x²(2) + 8x(x) + 8x(2) + 5(x) + 5(2)

= 3x³ + 6x² + 8x² + 16x + 5x + 10

= 3x³  + 14x² + 21x + 10

Example 6 :

(4x + 1)(3x - 1)(x + 1)

Solution :

By expanding first two factors, we get

= [4x(3x) - 4x(1) + 1(3x) - 1(1)] (x + 1)

= (12x² - 4x + 3x - 1) (x + 1)

= (12x² - x - 1) (x + 1)

= 12x²(x) + 12x²(1) - x(x) - x(1) - 1(x) - 1(1)

= 12x³ + 12x² - x² - x - x - 1

= 12x³  + 11x² - 2x - 1

Example 7 :

(2 - x)(3x + 1)(x - 7)

Solution :

By expanding first two factors, we get

= [2(3x) + 2(1) - x(3x) - x(1)] (x - 7)

= (6x + 2 - 3x² - x) (x - 7)

= (-3x² + 5x + 2) (x - 7)

= -3x²(x) + 3x²(7) + 5x(x) - 5x(7) + 2(x) - 2(7)

= -3x³ + 21x² + 5x² - 35x + 2x - 14

= -3x³  + 26x² - 33x - 14

Example 8 :

(x - 2)(4 - x)(3x + 2)

Solution :

By expanding first two factors, we get

= [x(4) - x(x) - 2(4) + 2(x)] (3x + 2)

= (4x - x² - 8 + 2x) (3x + 2)

= (-x² + 6x - 8) (3x + 2)

= -x²(3x) - x²(2) + 6x(3x) + 6x(2) - 8(3x) - 8(2)

= -3x³ - 2x² + 18x² + 12x - 24x - 16

= -3x³  + 16x² - 12x - 16

Example 9 :

The area A of a trapezoid is one half the height h times the sum of the bases b₁ and b₂. Write the expression for the area of the trapezoid.

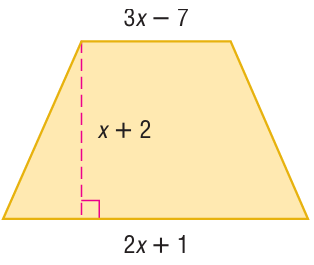
Solution :

Area of trapezoid = (1/2) ⋅ h(a + b)

Height = x + 2, a = 2x + 1 and b = 3x - 7

= (1/2) ⋅ (x + 2) (2x + 1 + 3x - 7)

= (1/2) ⋅ (x + 2) (5x - 6)

= (1/2) ⋅ (5x² - 6x + 10x - 12)

= (1/2) ⋅ (5x² + 4x - 12)

So, area of the trapezoid is (1/2) ⋅ (5x² + 4x - 12) square units.

Example 10 :

A homeowner is installing a swimming pool in his backyard. He wants its length to be 4 feet longer than its width. Then he wants to surround it with a concrete walkway 3 feet wide. If he can only afford 300 square feet of concrete for the walkway, what should the dimensions of the pool be ?

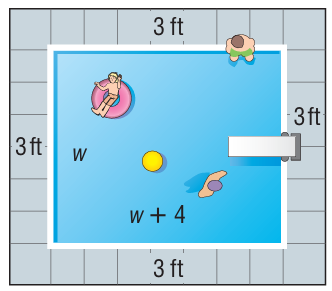
Solution :

Length of backyard = w + 4 + 3 + 3

= (w + 10) ft

Width of backyard = w + 3 + 3

= (w + 6) ft

Length of pool = w + 4

Width of pool = w

Area of concrete = Area of backyard - area of pool

= (w + 10)(w + 6) - w(w + 4)

= w² + 6w + 10w + 60 - w² - 4w

= 6w + 10w - 4w + 60

300 = 12w + 60

300 - 60 = 12w

w = 240 / 12

w = 20

Length of pool = 20 + 4 ==> 24 ft

Width of pool = 20 ft