MULTIPLYING BINOMIAL BY TRINOMIAL

Expand and simplify :

Example 1 :

(x + 2)(x² + x + 4)

Solution :

By distributing x and 2, we get

= x(x²) + x(x) + x(4) + 2(x²) + 2(x) + 2(4)

= x³ + x² + 4x + 2x² + 2x + 8

= x³ + 3x² + 6x + 8

Example 2 :

(x + 3)(x² + 2x - 3)

Solution :

By distributing x and 3, we get

= (x + 3)(x² + 2x - 3)

= x(x²) + x(2x) - x(3) + 3(x²) + 3(2x) - 3(3)

= x³ + 2x² - 3x + 3x² + 6x - 9

= x³ + 5x² + 3x - 9

Example 3 :

(x + 3)(x² + 2x + 1)

Solution :

By distributing x and 3, we get

= (x + 3)(x² + 2x + 1)

= x(x²) + x(2x) + x(1) + 3(x²) + 3(2x) + 3(1)

= x³ + 2x² + x + 3x² + 6x + 3

= x³ + 5x² + 7x + 3

Example 4 :

(x + 1)(2x² - x - 5)

Solution :

By distributing x and 1, we get

= (x + 1)(2x² - x - 5)

= x(2x²) - x(x) - x(5) + 1(2x²) - 1(x) - 1(5)

= 2x³ - x² - 5x + 2x² - x - 5

= 2x³ + x² - 6x - 5

Example 5 :

(2x + 3)(x² + 2x + 1)

Solution :

By distributing 2x and 3, we get

= (2x + 3)(x² + 2x + 1)

= 2x(x²) + 2x(2x) + 2x(1) + 3(x²) + 3(2x) + 3(1)

= 2x³ + 4x² + 2x + 3x² + 6x + 3

= 2x³ + 7x² + 8x + 3

Example 6 :

(2x - 5)(x² - 2x - 3)

Solution :

By distributing 2x and 5, we get

= (2x - 5)(x² - 2x - 3)

= 2x(x²) - 2x(2x) - 2x(3) - 5(x²) + 5(2x) + 5(3)

= 2x³ - 4x² - 6x - 5x² + 10x + 15

= 2x³ - 9x² + 4x + 15

Example 7 :

(x + 5)(3x² - x + 4)

Solution :

By distributing x and 5, we get

= (x + 5)(3x² - x + 4)

= x(3x²) - x(x) + x(4) + 5(3x²) - 5(x) + 5(4)

= 3x³ - x² + 4x + 15x² - 5x + 20

= 3x³ + 14x² - x + 20

Example 8 :

(4x - 1)(2x² - 3x + 1)

Solution :

By distributing 4x and 1, we get

= (4x - 1)(2x² - 3x + 1)

= 4x(2x²) - 4x(3x) + 4x(1) - 1(2x²) + 1(3x) - 1(1)

= 8x³ - 12x² + 4x - 2x² + 3x - 1

= 8x³ - 14x² + 7x - 1

Example 9 :

A hotel installs a new swimming pool and a new hot tub.

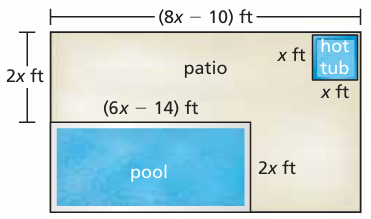
a. Write the polynomial in standard form that represents the area of the patio.

b. The patio will cost $10 per square foot. Determine the cost of the patio when x = 9.

Solution :

a)

Area of patio = Area of hotel - (area of pool + area of hot tub)

Dimension of hotel :

Length = (8x - 10) ft

width = 4 ft

Dimensions of pool :

Length = (6x - 14) ft

width = 2 x ft

Dimensions of hot tub :

length = width = x ft

Area of patio = (8x - 10)4x - [2x(6x - 14) + x(x)]

= 32x² - 40x - [12x² - 28x + x²]

= 32x² - 40x - 12x² + 28x - x²

= 32x² - 12x² - x² - 40x + 28x

Area of patio = 19x² - 12x

b)

Cost, when x = 10

Total cost = 19(10)² - 12(10)

= 19 (100) - 120

= 1900 - 120

= 1780

Example 10 :

hockey, a goalie behind the goal line can only play a puck in the trapezoidal region.

a. Write a polynomial that represents the area of the trapezoidal region.

b. Find the area of the trapezoidal region when the shorter base is 18 feet.

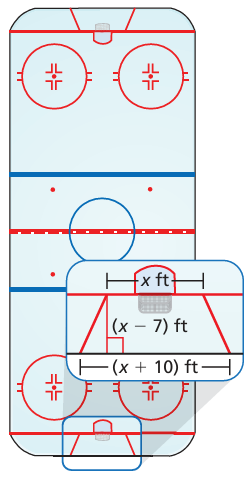
Solution :

a)

Height = x - 7, bases a = x + 10, b = x

Area of trapezoid = (1/2) h(a + b)

= (1/2) (x - 7) (x + 10 + x)

= (1/2)(x - 7) (2x + 10)

= (1/2) 2(x - 7) (x + 5)

= (x - 7)(x + 5)

= x² + 5x - 7x - 35

= x² - 2x - 35

Area of trapezoid = x² - 2x - 35 square units

b)  Shorter base x = 18 ft

x + 10 = 18 + 10 ==> 28 ft

x - 7 = 18 - 7 ==> 11 ft

= (1/2) 11(28 + 18)

= (1/2) x 11 x 46

= 11 x 23

= 253 sqaure ft

Example 11 :

The football field is rectangular

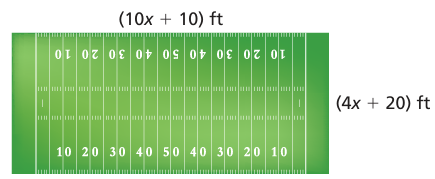
a. Write a polynomial that represents the area of the football field.

b. Find the area of the football field when the width is 160 feet.

Solution :

a)  Area of foot bal field = (4x + 20)(10x + 10)

= 40x² + 40x + 200x + 200

= 40x² + 240x + 200

b)  Applying x = 160

= 40(160)² + 240(160) + 200

= 40(25600) + 38400 + 200

= 1024000 + 38400 + 200

= 1062600 square ft

Example 12 :

The shipping container is a rectangular prism. Write a polynomial that represents the volume of the container

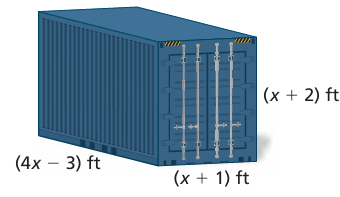
Solution :

Length = 4x - 3

Width = x + 1

height = x + 2

Volume of the container = length (width)(height)

= (4x - 3) (x + 1)(x + 2)

= (4x - 3)(x² + 2x + x + 2)

= (4x - 3)(x² + 3x + 2)

= 4x³  + 12x² + 8x - 3x² - 9x - 6

= 4x³  + 9x² - 9x - 6