MULTIPLYING AND DIVIDING FUNCTIONS

Find

(i)  (fg)(x)

(II)  (f/g)(x)

and state the domain of each. Then evaluate fg and f/g for the given value of x.

Problem 1 :

f(x) = 2x³, g(x) = ∛x; x = -27

Solution :

f(x) = 2x³, g(x) = ∛x and x = -27

(i)  (f × g)x = f(x) × g(x)

(f × g)x =  2x³ × ∛x

When, x = -27

(f × g)(-27) = 2(-27)³ × ∛(-27)

= -39366 × ∛(-3 ⋅ -3 ⋅ -3)

= -39366 × (-3)

(f × g)(-27) = -118098

(ii)  (f/g)x = f(x)/g(x)

(f/g)(x) = 2x³/∛x

(f/g)(-27) = 2(-27)³/∛(-27)

= -39366 / ∛(-3 ⋅ -3 ⋅ -3)

= -39366/(-3)

(f/g)(-27) = 13122

Problem 2 :

f(x) = x⁴, g(x) = 3√x; x = 4

Solution :

f(x) = x⁴ , g(x) = 3√x and x = 4

(i) (f × g)x = f(x) × g(x)

(f × g)x = x⁴ × 3√x

When, x = 4

(f × g)(4) = (4)⁴ × 3√4

= 256 × 3√(2 ⋅ 2)

= 256 × 3(2)

= 256 × 6

(f × g)(4) = 1536

(ii)  (f/g)x = f(x)/g(x)

(f/g)(4) = (4)⁴/3√4

= 256/3√(2 ⋅ 2)

= 256/3(2)

(f/g)x = 256/6

Problem 3 :

f(x) = 4x, g(x) = 9x^1/2; x = 9

Solution :

f(x) = 4x, g(x) = 9x^1/2 and x = 9

(i)  (f × g)x = f(x) × g(x)

(f × g)x = 4x × 9x^1/2

When, x = 9

(f × g)(9) = 4(9) × 9(9)^1/2

= 36 ×  9(3²)^1/2

= 36 × 27

 (f × g)(4) = 972

(ii)  (f/g)x = f(x)/g(x)

(f/g)(9) = 4(9)/9(9)^1/2

= 36/9(3²)^1/2

(f/g)(x) = 36/27

Problem 4 :

f(x) = 11x³, g(x) = 7x^7/3; x = -8

Solution :

f(x) = 11x³, g(x) = 7x^7/3 and x = -8

(i) (f × g)x = f(x) × g(x)

(f × g)x = 11x³ × 7x^7/3

(f × g)x = 77x^3+7/3

(f × g)x = 77x^16/3

(f × g)(-8) = 77(-8)^16/3

(f × g)(-8) = 77(-2)^3(16/3)

(f × g)(-8) = 77(-2)¹⁶

(ii)  (f/g)x = f(x)/g(x)

(f /g)x = 11x³ /  7x^7/3

(f/g)x = (11/7)x^3-7/3

(f/g)x = (11/7)x^(9-7)/3

(f/g)x = (11/7)x^2/3

(f/g)(-8) = (11/7)(-8)^2/3

(f/g)(-8) = (11/7)(-2)²

(f/g)(-8) = 44/7

Problem 5 :

f(x) = 7x^3/2, g(x) = -14x^1/3; x = 64

Solution :

Given, f(x) = 7x^3/2

 g(x) = -14x^1/3

 x = 64

(i) (f × g)x = f(x) × g(x)

(f × g)x =  7x^3/2 × (-14x^1/3)

When, x = 64

(f × g)(64) = 7(64)^3/2 × (-14(64)^1/3)

(f × g)(64) = 7(8²)^3/2 × (-14(4³)^1/3)

= 7(8)³ × (-14(4))

= 7(512) × (-56)

= 3584 × (-56)

(f × g)(64) = -200704

(ii) (f/g)x = f(x)/g(x)

(f/g)(x) = 7(64)^3/2/(-14(64)^1/3)

(f/g)(64) = 7(8²)^3/2/(-14(4³)^1/3)

= 7(8)³/(-14(4))

= 7(512)/(-56)

= 3584/(-56)

 (f/g)(64) = -64

Problem 6 :

f(x) = 4x^5/4, g(x) = 2x^1/2; x = 16

Solution :

Given, f(x) = 4x^5/4

g(x) = 2x^1/2

x = 16

(i) (f × g)x = f(x) × g(x)

(f × g)x = 4x^5/4 × 2x^1/2

When, x = 16

(f × g)(16) = 4(16)^5/4 × 2(16)^1/2  

= 4(2⁴)^5/4 × 2(4²)^1/2  

 = 4(2)⁵ × 2(4)

= 128 × 8

(f × g)(16) = 1024   

(ii)  (f/g)x = f(x)/g(x)

(f/g)(x) = 4x^5/4/ 2x^1/2

(f/g)(x) = 2x^{5/4 - 1/2}

(f/g)(x) = 2x^3/4

(f/g)(16) = 2(16)^3/4

(f/g)(16) = 2(2⁴)^3/4

(f/g)(16) = 2(2³)

(f/g)(16) = 16

Problem 7 :

Find (fg)(2) when f(x) = x - 6 and g(x) = -3x² + 11x - 7

a)  -152     b)  24    c) -12     d) -76

Solution :

f(x) = x - 6 and g(x) = -3x² + 11x - 7

(f g)(2) = f(2) g(2)

= -4(3)

= -12

So, the value of (f g)(2) is -12.

Problem 8 :

Find (f/g) (-5) when f(x) = 4x - 2 and g(x) = 5x² + 14x + 2.

a)  - 22/57     b) 4/57      c) 5/57     d) 5/18

Solution :

f(x) = 4x - 2 and g(x) = 5x² + 14x + 2.

(f/g) (-5) = f(-5) / g(-5)

(f/g) (-5) = -22 / (-8)

= 11/4

Problem 9 :

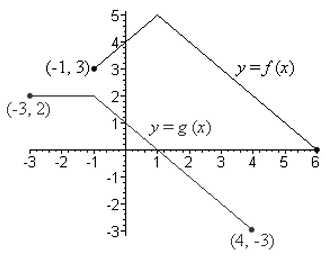
The graphs of two functions f and g are shown. Find the following :

a) (f - g) (-1)

b)  (f g) (1)

c)  The domain of (f + g) (x) and the domain of (f/g) (x)

Solution :

a)

(f - g) (-1) = f(-1) - g(-1)

= 3 - 2

= 1

b) 

(f g) (1) = f(1) g(1)

= 5 (0)

= 0

c)  By observing the graph, the domain of the function f is [-1, 6]

By observing the graph, the domain of the function g is [-3, 4]

The domain of (f + g) (x) = [-1, 6] n [-3, 4] is [-1, 4].

Domain of (f/g) (x) :

g(1) = 0

In the domain [-1, 4] we should exclude the value 1, so the domain is [-1, 1) and (1, 4].