MODELLING EXPONENTIAL GROWTH AND DECAY

Problem 1 :

A flu outbreak hits your school on Monday, with an initial number of 20 ill students coming to school. The number of ill students increases by 25% per hour.

a) Is this an example of exponential growth or decay?

b) Write an exponential function to model this Monday flu outbreak.

c) How many students will be ill after 6 hours?

Solution:

Given, initial number of ill students = 20

Rate of increasing = 25%

a)

Exponential growth

b) 

y = ab^x

a = initial,  b = (1 + r) growth factor  

y = 20(1 + 0.25)^x

c) 

x = 6 hours

y = 20(1.25)⁶

y = 76.2939

So, 76 ill  students.

Problem 2 :

A total of 50,000 contestants participate in an internet on-line survivor game. The game randomly kills off 20% of the contestants each day.

a) Is this an example of exponential growth or decay?

b) Write an exponential function to model this game.

c) How many contestants are left in the game at the end of one week?

Solution:

a)

Exponential decay

b) 

y = 50000(1 - 20%)^x

y = 50000(0.8)^x

c) 

x = 1 week

y = 50000(0.8)⁷

y = 10485.76

y ≈ 10486 contestants

Problem 3 :

A new sports car sells for $35,000/. The value of the car decreases by 18% annually. Which of the following choices models the yearly value of the car since its purchase?

1) y = 35000(1.18)^x           2) y = 35000(.82)^x

3) y = 35000(.18)^x               4) y = 35000(-0.18)^x

Solution:

y = 35000(1 - 18%)^x

y = 35000(1 - 0.18)^x

 y = 35000(0.82)^x

So, option (2) is correct.

Problem 4 :

At the end of last year, the population of Jason's hometown was approximately 75,000 people. The population is growing at the rate of 2.4% each year. Which equation models the growth?

1) y = 75000(1.24)^x             2) y = 75000(1.024)^x

3) y = 75000(.76)^x               4) y = 75000(.976)^x

Solution:

y = 75000(1 + 2.4%)^x

y = 75000(1 + 0.024)^x

y = 75000(1.024)^x

So, option (2) is correct.

Problem 5 :

The world population in 2000 was approximately 6.08 billion. The annual rate of increases was about 1.26%.

a. Find the growth factor for the world populations.

b. Suppose the rate of increase continues to be 1.26%. Write a function to model the world population.

c. Let x be the number of years past the year 2000. Find the world population in 2010.

Solution:

a.

The rate of growth for the word population is 1.26%.

b. 

Let x be the number of years past the year 2000.

P = 6.08(1 + 1.26%)^x

c. 

x = 10

P = 6.08(1 + 1.26%)¹⁰

= 6.08(1 + 0.0126)¹⁰

P = 6.89 billion

Problem 6 :

A computer valued at $6500 depreciates at the rate of 14.3% per year.

a. Write a function that models the value of the computer.

b. Find the value of the computer after three years.

Solution:

Given, Initial value = $6500

Rate of depreciation = 14.3% = 0.143

A = P(1 - r)^t

A = 6500(1 - 0.143)^t

A = 6500(0.0857)^t

a)

Function that model the value of computer.

y = 6500(0.857)^x

b) 

 x = 3

y = 6500(0.857)³

y = 4091.25

Thus, value of after 3 years is $4091.25.

Problem 7 :

The population of a certain animal species decreases at a rate of 3.5% per year. You have counted 80 of the animals in the habitat you are studying.

a. Write a function that models the change in the animal population.

b. Graph the function. Estimate the number of years until the population fist drops below 15 animals.

Solution:

a)

A = P(1 + r)^t

P = 80

r = -3.5% = -0.035

t = number of time period

A = 80(1 - 0.035)^t

A = 80(0.965)^t

b) 

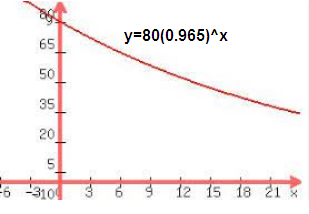
Let y = 15

15 = 80(0.965)t

0.1875 = (0.965)t

t log(0.965) = log(0.1875)

t = 47 years