MODELLING WITH LINEAR FUNCTIONS

Problem 1 :

Which chart could represent the function f(x) = -2x + 6?

Solution:

1) For the first chart:

-2 × 0 + 6 = 6 = 6 

-2 × 2 + 6 = 2 ≠ 10

-2 × 4 + 6 = -2 ≠ 14

-2 × 6 + 6 = -6 ≠ 18

2) For the second chart:

-2 × 0 + 6 = 6 ≠ 4

-2 × 2 + 6 = 2 ≠ 6

-2 × 4 + 6 = -2 ≠ 8

-2 × 6 + 6 = -6 ≠ 10

3) For the third chart:

-2 × 0 + 6 = 6 ≠ 8 

-2 × 2 + 6 = 2 ≠ 10

-2 × 4 + 6 = -2 ≠ 12

-2 × 6 + 6 = -6 ≠ 14

4) For the fourth chart:

-2 × 0 + 6 = 6 = 6 

-2 × 2 + 6 = 2 = 2

-2 × 4 + 6 = -2 = -2

-2 × 6 + 6 = -6 = -6

The fourth chart could represent the function.

So, option (4) is correct.

Problem 2 :

Which equation expresses the relationship between a and y, as shown in the accompanying table?

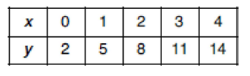
1) y = x + 3      2) y = 2x + 3   3) y = 3x + 2    4) y = x + 2

Solution:

Let equation is y = mx + c

Substitute the values of x and y

(x, y) = (0, 2) ==> 2 = m(0) + c

c = 2

(x, y) = (1, 5) ==> 5 = m(1) + c

5 = m + c

5 = m + 2

m = 3

So, equation is y = 3x + 2

So, option (3) is correct.

Problem 3 :

If x and y are defined as indicated by the accompanying table, which equation correctly represents the relationship between x and y?

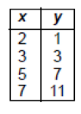
1) y = x + 2          2) y = 2x + 2         3) y = 2x + 3

4) y = 2x - 3

Solution:

1)

If x = 2,

y = 2 + 2 

y = 4

It is false.

2) 

If x = 2,

y = 2(2) + 2

y = 6

It is false.

3)

If x = 2

y = 2(2) + 3

y = 7

It is false.

4)

If x = 2

y = 2(2) - 3

y = 1

It is true.

So, option (4) is correct.

Problem 4 :

Which linear equation represents the data in the accompanying table?

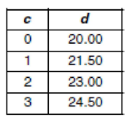
1) d = 1.50c      2) d = 1.50c + 20.00     3) d = 20.00c + 1.50

4) d = 21.50c

Solution:

The linear equation y = mx + c

d = kc + b

k = (21.5 - 20)/(1 - 0)

= 1.5

(0, 20)

b = 20

d = 1.50c + 20.00

So, option (2) is correct.

Problem 5 :

Each day Toni records the height of a plant for her science lab. Her data are shown in the table below.

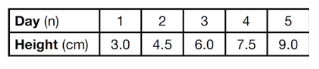
The plant continues to grow at a constant daily rate. Write an equation to represent h(n), the height of the plant on nth day.

Solution:

h(n) = 1.5(n - 1) + 3.0

= 1.5n - 1.5 + 3.0

h(n) = 1.5n + 1.5

Problem 6 :

Tanya is making homemade greeting cards. The data table below represents the amount she spends in dollars, f(x), in terms of the number of cards she makes, x.

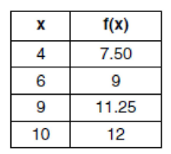
Write a linear function, f(x), that represents the data. explain what the slope and y-intercept of f(x) mean in the given context.

Solution:

1)

f(x) = kx + b

b = f(x) - kx

= 7.50 - 4(0.75)

= 4.50

f(x) = 4.50 + 0.75x

2)

k = 0.75x means per cards is 0.75 dollars.

b = 4.50 means cost price.

Problem 7 :

Which equation is represented by the graph below?

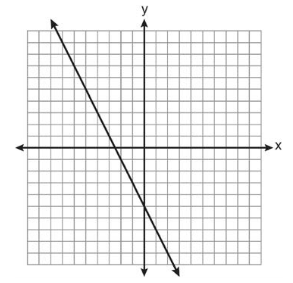
1) 2y + x = 10       2) y - 2x = -5     3) -2y = 10x - 4

4) 2y = -4x - 10

Solution:

x intercept = (-2.5, 0)

y intercept = (0, -5)

So, option (4) is correct.

Problem 8 :

Write the equation for the line shown in the accompanying graph. Explain your answer.

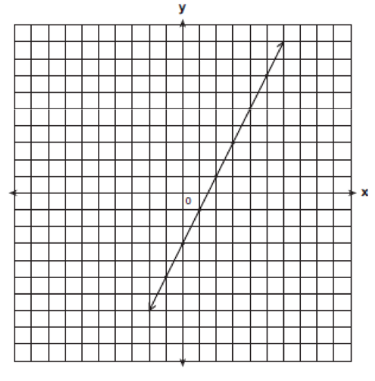
Solution:

y = 2x - 3

The y- intercept is -3.

The line has a slope of 2.

The equation for the line is y = 2x - 3.