MODELING WITH LINEAR EQUATIONS WORD PROBLEMS

Problem 1 :

The table shows the height of a bamboo shoot during a period of fast growth. Use the table to write an equation modeling the growth. 

Solution :

When x = 0 and y = 15. So, y-intercept = 15.

Rate of change :

m = (y₂ - y₁)/(x₂ - x₁)

m = (16.5 - 15)/(1 - 0)

m = 1.5

Problem 2 :

Your cell phone plan costs $40 per month plus $0.10 per text message. You receive a bill for $53.80.

a) Writing a Model Write an equation for the situation. Solve it to find exactly how many text messages you sent.

b) Making a Table Copy and complete the table below. Use the table to estimate how many text messages you sent.

Solution :

a) Let x be the number of text messages and y be the bill amount.

y = 40 + 0.10x ------(1)

Bill amount (y) = 53.80

53.80 = 40 + 0.10x

Subtract 40 on both sides.

53.80 - 40 = 0.10x

0.10x = 13.8

x = 13.8/0.10

x = 138

So, the number of text messages sent is 138.

b) Apply x = 50, x = 100, x = 15 and x = 200 in (1), we get

Problem 3 :

A paramotor is a parachute propelled by a fan-like motor. The table shows the height h of a Para motorist t minutes after beginning a descent. Find the height of the Para motorist after 7 minutes.

Solution :

The height decreases by 250 feet per minute.

Initial height = 2000

Let h be the height.

Rate of change(m) = -250

h = -250x + 2000

Height after 7 minutes.

When x = 7

h = -250(7) + 2000

h = -1750 + 2000

h = 250

So, height after 7 minutes is 250 feet.

Problem 4 :

A car used 14 gallons of gasoline and traveled a total distance of 550 miles. The car’s fuel efficiency is 40 miles per gallon on the highway and 35 miles per gallon in the city. How many gallons of gasoline were used on the highway?

Solution :

Quantity of gasoline used = 14

Distance covered = 550 miles

Fuel efficiency in highway = 40 miles

Let g be the number of gallons used in highway. Then, (14-g) is the quantity of fuel used in city.

Fuel efficiency in city = 35 miles

550 = 40g + 35(14-g)

Solving the equation, we get

550 = 40g + 490 - 35g

550 = 5g + 490

550 - 490 = 5g

g = 60/5

g = 12

So, the car used 12 gallons in highway.

Problem 5 :

The table shows the height h of a para motorist after t minutes. Find the height of the para motorist after 8 minutes

Solution :

For every one minute, the height decreases.

Rate of change (m) = (2190 - 2400)/(1 - 0)

m = 210

y = 2400 - 210x

Height after 8 minutes

y = 2400 - 210(8)

y = 2400 - 1680

y = 720 ft

Problem 6 :

You have $110 in your lunch account and plan to spend $2.75 each school day.

a. Write and graph a linear equation that represents the balance in your lunch account.

b. How many school days will it take to spend all of the money in your lunch account?

Solution :

• Let x be the number of days to be spent.
• Let y be the total amount.

Initial amount you have is $110

y = 110 - 2.75x

a)

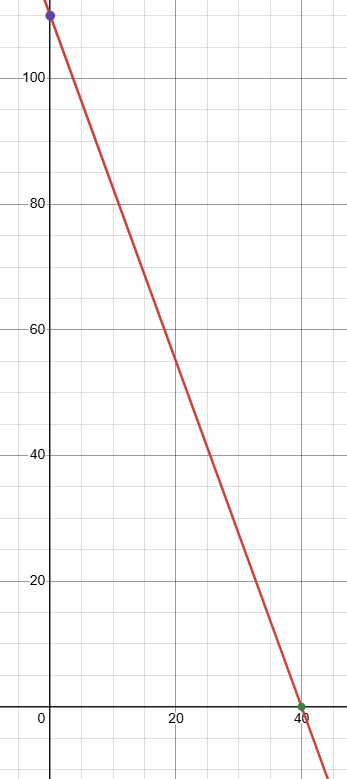
b)  y = 0

110 - 2.75x = 0

2.75x = 110

x = 110/2.75

x = 40

So, the required number of days is 40.

Problem 7 :

You secure an interest-free loan to purchase a boat. You agree to make equal monthly payments for the next two years. The graph shows the amount of money you still owe.

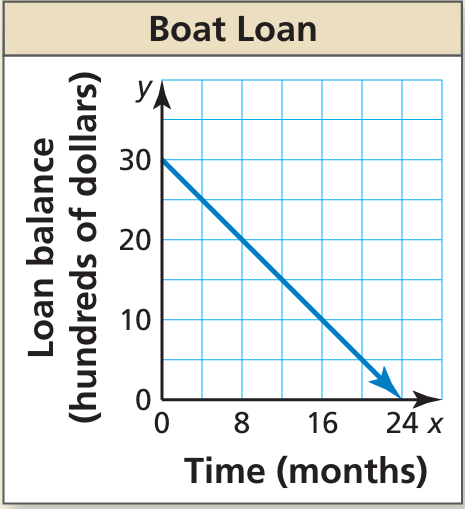
a. What is the slope of the line? What does the slope represent?

b. What is the domain and range of the function? What does each represent?

c. How much do you still owe after making payments for 12 months?

Solution :

a) 

Choosing two points on the line (8, 20) and (16, 10)

Slope = (10 - 20) / (16 - 8)

= -10/8

= -5/4

Decreasing rate is 1.25.

b)  y = 30 - 1.25x

When y = 0

1.25x = 30

x = 30/1.25

x = 24

Domain (0, 24) and range (0, 30)

c) Amount after 12 months.

y = 30 - 1.25(12)

= 30 - 15

= 15

We have to owe 15 (hundred of dollars).

Problem 8 :

The graph shows the remaining balance y on a car loan after making x monthly payments. Write an equation of the line and interpret the slope and y-intercept. What is the remaining balance after 36 payments?

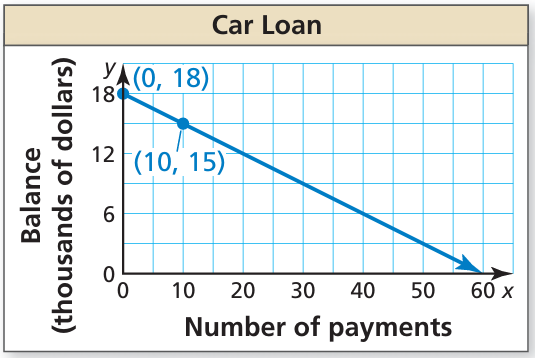
Solution :

Slope of the line :

(0, 18) and (10, 15)

Slope = (15 - 18) / (10 - 0)

= -3/10

Equation of the line :

Initial balance = 18000

y = 18 - (3/10)x

Amount paid in 36 months 

y = 18 - (3/10)(36)

= 18 - 10.8

y = 7.2

Remainding amount to be paid = 18 - 7.2

= 10.8

10.8 = 18 - (3/10)x

(3/10)x = 18 - 10.8

(3/10)x = 7.2

x = 7.2(10/3)

x = 24

So, the required number of payments is 24.