MIDPOINTOF THE LINE SEGMENT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find the midpoint of the line segment, we will use the formula
= [(x1 + x2)/2 , (y1 + y2)/2]
(x1, y1) and (x2, y2) are the endpoints of the line segment.
Problem 1 :
The endpoints of RS are R(1, -3) and S(4, 2). Find the coordinates of the Midpoint M.
Solution :
Given, R(1, -3) and S(4, 2)
Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = 1, y1 = -3, x2 = 4, y2 = 2
= (1 + 4)/2 , (-3 + 2)/2
= (5/2 , -1/2)
So, the coordinates of the Midpoint M = (5/2, -1/2)
Problem 2 :
The midpoint of JK is M(2, 1). One endpoint is J(1, 4). Find the coordinates of endpoint K.
Solution :
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
Given, M(2, 1) and One endpoint is J(1, 4)
x1 = 1, y1 = 4, x2 = x2, y2 = y2
(2, 1) = [(1 + x2)/2, (4 + y2)/2]
Equating the x and y-coordinates, we get
|
(1 + x2)/2 = 2 1 + x2 = 4 x2 = 4 - 1 x2 = 3 |
(4 + y2)/2 = 1 4 + y2 = 2 y2 = 2 - 4 y2 = -2 |
So, the coordinates of endpoint K = (3, -2).
Problem 3 :
The endpoints of AB are A(1, 2) and B(7, 8). Find the coordinates of the midpoint M.
Solution :
Given, A(1, 2) and S(7, 8)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = 1, y1 = 2, x2 = 7, y2 = 8
= [(1 + 7)/2 , (2 + 8)/2]
= [8/2 , 10/2]
= [4, 5]
So, the coordinates of the midpoint M = [4, 5].
Problem 4 :
The midpoint of VW is M(-1, -2). One endpoint is W(4, 4). Find the coordinates of endpoint V.
Solution :
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
Given, M(-1, -2) and One endpoint is W(4, 4)
x1 = 4, y1 = 4, x2 = x2, y2 = y2
(-1, -2) = [(4 + x2)/2, (4 + y2)/2]
Equating the x and y-coordinates, we get
|
(4 + x2)/2 = -1 4 + x2 = -2 x2 = -2 - 4 x2 = -6 |
(4 + y2)/2 = -2 4 + y2 = -4 y2 = -4 - 4 y2 = -8 |
So, the coordinates
of endpoint K = (-6, -8).
Find the coordinates of the midpoint of the segment with the given endpoints.
Problem 5 :
C(3, 5) and D(7, 5)
Solution :
Given, C(3, 5) and D(7, 5)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = 3, y1 = 5, x2 = 7, y2 = 5
= [(3 + 7)/2 , (5 + 5)/2]
= (10/2 , 10/2)
= (5, 5)
So, the coordinates of the Midpoint is (5, 5).
Problem 6 :
E(0, 4) and F(4, 3)
Solution :
Given, E(0, 4) and F(4, 3)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = 0, y1 = 4, x2 = 4, y2 = 3
= (0 + 4)/2 , (4 + 3)/2
= (4/2 , 7/2)
= (2, 7/2)
So, the coordinates of the Midpoint M = (2, 7/2)
Problem 7 :
G(-4, 4) and H(6, 4)
Solution :
Given, G(-4, 4) and H(6, 4)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = -4, y1 = 4, x2 = 6, y2 = 4
= [(-4 + 6)/2 , (4 + 4)/2]
= [2/2 , 8/2]
= [1, 4]
So, the coordinates of the Midpoint M = [1, 4].
Problem 8 :
J(-7, -5) and K(-3, 7)
Solution :
Given, J(-7, -5) and K(-3, 7)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = -7, y1 = -5, x2 = -3, y2 = 7
= [(-7 - 3)/2 , (-5 + 7)/2]
= [-10/2 , 2/2]
= [-5, 1]
So, the coordinates of the Midpoint M = [-5, 1].
Problem 9 :
P(-8, -7) and Q(11, 5)
Solution :
Given, P(-8, -7) and Q(11, 5)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = -8, y1 = -7, x2 = 11, y2 = 5
= [(-8 + 11)/2 , (-7 + 5)/2]
= [3/2 , -2/2]
= [1.5, -1]
So, the coordinates of the Midpoint M = [1.5, -1].
Problem 10 :
S(-3, 3) and T(-8, 6)
Solution :
Given, S(-3, 3) and T(-8, 6)
Coordinates of the Midpoint M = [(x1 + x2)/2 , (y1 + y2)/2]
x1 = -3, y1 = 3, x2 = -8, y2 = 6
= (-3 - 8)/2 , (3 + 6)/2
= (-11/2 , 9/2)
So, the coordinates of the Midpoint M = (-11/2 , 9/2).
Problem 11 :
The endpoints of 𝑃𝑄 are 𝑃(3, −4) and 𝑄(11, 𝑐). The midpoint of 𝑃𝑄 is 𝑀(𝑑, 3). Find the values of 𝑐 and 𝑑.
Solution :
M = midpoint of PQ
𝑃(3, −4) and 𝑄(11, 𝑐).
(d, 3) = (3 + 11)/2, (-4 + c)/2
(d, 3) = 14/2, (-4 + c)/2
(d, 3) = 7, (-4 + c)/2
Equating the x and y co-ordinates, we get
d = 7
(-4 + c)/2 = 3
-4 + c = 6
c = 6 + 4
c = 10
So, the values of c and d are 7 and 10 respectively.
Problem 12 :
M is the midpoint of each segment. Set up an equation to find x and then find the specified lengths.
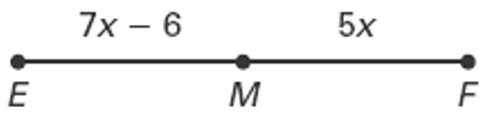
Solution :
M is the midpoing of the line segment.
EM = MF
7x - 6 = 5x
7x - 5x = 6
2x = 6
x = 6/2
x = 3
So, the value of x is 3.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling