MENSURATION AREA PROBLEMS WITH INSCRIBED SHAPES

Problem 1 :

The area of the circle that can be inscribed in a square of side 6 cm is :

a) 36π cm²     (b) 18π cm²  (c) 12π cm²      (d) 9π cm² 

Solution :

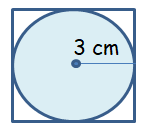
Radius of the circle = 3 cm

Area of the circle = πr²

= π (3)²

= 9π cm²

So, area of the required circle is 9π cm².

Problem 2 :

The area of the square that can be inscribed in a circle of radius 8 cm is :

(a) 256 cm²      (b) 128 cm²      (c) 64 2 cm²     (d) 64 cm² 

Solution :

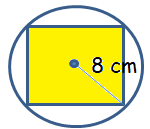
Diameter of the circle = diagonal of the square

Length of diagonal = 16 cm

Let x be the side length of the square

x² + x² = 16²

2x² = 256

x² = 128

x = √(2 x 2 x 2 x 2 x 2 x 2 x 2)

x = 8√2 (side length of the square)

Area of the square = x² = 128 cm²

Problem 3 :

Area of the largest triangle that can be inscribed in a semi-circle of radius r units is :

a) r² sq.units     b) (1/2) r² sq.units   c) 2r² sq.units

d) √2 r² sq.units

Solution :

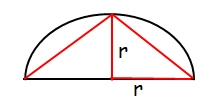
Area of the triangle = (1/2) x base x height

= (1/2) x r x r

= (1/2) r² square units

Problem 4 :

The circumference of the circle is 100 cm. Find the side of the square inscribed in the circle

Solution :

Circumference of the circle = 100 cm

2π r = 100

r = 100 x (1/2) x (7/22)

r = 15.9

Approximately the radius of the circle is 16 cm

When square inscribed in the circle, there must be a relationship between side length of the square and diameter of the circle. They will be equal.

2(radius) = diameter = 2(16) ==> 32 cm

Problem 5 :

The area of the circle that can be inscribed in a square of the side 6 cm is 

Solution :

Here the circle inscribed in a square. 

Diameter of the circle = Side length of the square

2r = 6

r = 3

Radius of the circle is 3 cm

Area of the circle = π r²

= π (3)²

= 9π cm²

Problem 6 :

In the figure, a circle is inscribed in a square of side 6 cm and another circle is circumscribing the square. Is it true to say that area of the outer circle is two times the area of the inner circle? Give reasons for your answer

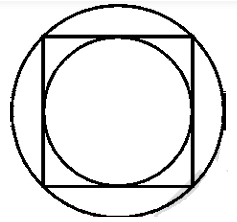
Solution :

The side length of the square is 6 cm

Diameter of the inner circle = 6 cm

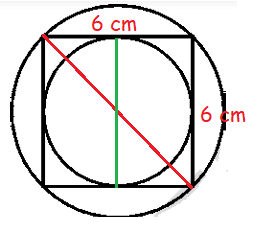
Diameter of the the larger circle that lies outside

6² + 6² = (diagonal of square)²

36 + 36 = (diagonal of square)² 

(diagonal of square)² = 72

(diagonal of square) = √72

Diagonal of the square = 6√2 = Diameter of the larger circle

Diameter of the smaller circle that lies inside = 6

Radius of the circle lies inside = 3 cm

Area of the smaller circle =  π r²

=  π (3)²

= 9 π square units

Radius of the larger circle = 6√2/2

= 3√2

Area of the larger circle =  π r²

=  π (3√2)²

= 18 π square units

Area of the outside circle = 2 area of the smaller circle

Problem 7 :

The area of a circle inscribed in an equilateral triangle is 154 cm². Find the perimeter of the triangle

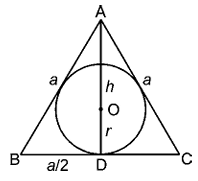
Solution :

Area of the circle =  π r²

 π r² = 154

 r² = 154 x (7/22)

 r² = 7 x 7

r = 7

Given ABC is an equilateral triangle and AD = h be the altitude.

Hence these bisectors are also the altitudes and medians whose point of intersection divides the medians in the ratio 2 : 1

∠ADB = 90° and OD = (1/3) AD

That is r = (h/3)

Þ h = 3r = 3 × 7 = 21 cm

Let each side of the triangle be a, then

Altitude of an equilateral triangle is (√3/2) times its side

That is h = (√3a/2)

a = 14√3 cm

Perimeter of the triangle = 3(14√3)

= 42√3 cm