MAXIMUM HEIGHT QUADRATIC WORD PROBLEMS

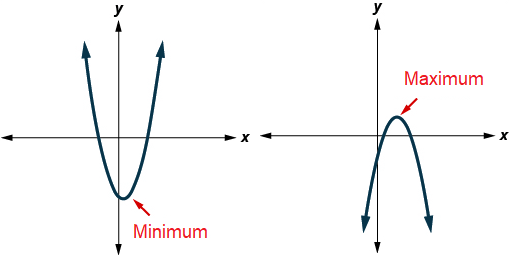
In general the graphical form of the quadratic function will the shape of u. It may be open upward or downward.

• Maximum point is the highest point of the parabolic path.
• Minimum point is the lowest point of the parabolic path.

To find maximum or minimum point of the quadratic equation we follow two ways.

(i) Converting into the vertex form

(ii) Using formula

Problem 1 :

An arrow is fired from a bow and its height, h, in metres above the ground, t seconds after being fired, is given by

ℎ(𝑡) = −5𝑡² + 40𝑡 + 3

Algebraically determine the maximum height attained by the arrow and the time taken to reach this height.

Solution :

ℎ(𝑡) = −5𝑡² + 40𝑡 + 3

Using completing the square method,

Step 1 :

Factor the coefficient of x² from the first two terms.

= -5(𝑡² - 8t) + 3

Step 2 :

Decompose the coefficient of t as multiple of 2

= -5[𝑡² - 2 t (4) + 4² - 4²] + 3

8t is broken into 2 x t x 4 and this is in the form of 2ab

Step 3 :

To complete this we add 4² and subtract 4²

= -5[(𝑡 - 4)² - 4²] + 3

= -5[(𝑡 - 4)² - 16] + 3

= -5(𝑡 - 4)² + 80 + 3

= -5(𝑡 - 4)² + 83

Maximum is at 4, the maximum value is 83.

So, the maximum height reached by the arrow is 83 meters and time taken for this is 4 seconds.

Problem 2 :

The path of a model rocket can be described by the quadratic function

𝑦 = −x² + 12x

where 𝑦 represents the height of the rocket, in meters, at time 𝑥 seconds after takeoff. Identify the maximum height reached by the rocket and determine the time at which the rocket reached its maximum height.

Solution :

𝑦 = −x² + 12x

𝑦 = −[x² - 12x]

𝑦 = −[x² - 2x(6) + 6² - 6²]

𝑦 = −[(x - 6)² - 6²]

𝑦 = −(x - 6)² + 36

vertex is at (6, 36)

Maximum height reached by the rocket is 36 meters after 6 seconds.

Problem 3 :

A baseball is hit and follows a parabolic path described by the function

ℎ(𝑡) = −3𝑡² + 12𝑡 + 1

where 𝑡 is time in seconds after the ball is hit and ℎ(𝑡) is the height of the ball above ground in metres. Algebraically determine the maximum height reached by the ball and the time it takes the ball to reach its maximum height.

Solution :

ℎ(𝑡) = −3𝑡² + 12𝑡 + 1

ℎ(𝑡) = −3[𝑡² - 4𝑡] + 1

ℎ(𝑡) = −3[𝑡² - 2𝑡(2) + 2² - 2²] + 1

ℎ(𝑡) = −3[(𝑡 - 2)² - 4] + 1

ℎ(𝑡) = −3(𝑡 - 2)² + 12 + 1

ℎ(𝑡) = −3(𝑡 - 2)² + 13

Vertex is at (2, 13)

The baseball will reach the maximum height after 2 seconds and the maximum height is 13 meters.

Problem 4 :

The height

ℎ = −16𝑡² + 64𝑡 + 190

in feet of an object above the ground is given by where t is the time in seconds. Find the time it takes the object to strike the ground and find the maximum height of the object.

Solution :

ℎ = −16𝑡² + 64𝑡 + 190

When it strikes the ground, h = 0

−16𝑡² + 64𝑡 + 190 = 0

t = 5.98 seconds

Maximum value :

h = −16𝑡² + 64𝑡 + 190

t = -b/2a

t = -64/2(-16) ==> 2

When t = 2, h = −16(2)² + 64(2) + 190

h = -64+128+190

h = 254

So, the maximum height is 254 feet.

Problem 5 :

The height in feet of a bottle rocket is given by

h(t) = 160t −16t²

where t is the time in seconds. How long will it take for the rocket to return to the ground? What is the height after 2 seconds?

Solution :

h(t) = 160t −16t²

h(t) = −16t² + 160t

When it reaches the ground, its height = 0

−16t² + 160t = 0

-16t(t - 10) = 0

t = 0 and t = 10

After 10 seconds it will reach the ground.

h(t) = 160t −16t²

t = 2

h(2) = 160(2) −16(2)²

= 320 - 64

= 256 ft

So, the height after 2 seconds is 256 ft.