MATH 1 PRACTICE TEST EOC WITH SOLUTIONS

Problem 31 :

The graph below shows the amount of profit, y, a company makes from selling x units of merchandise. 

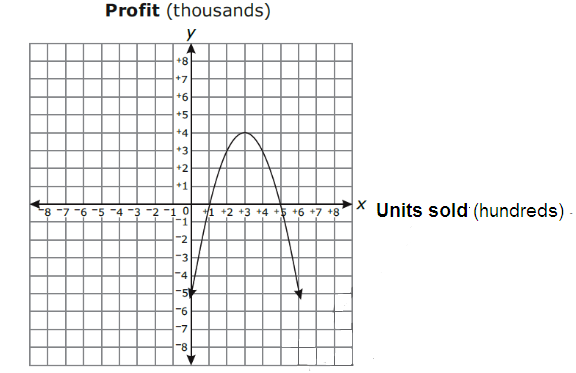
How many units of merchandise does the company need to sell to make the maximum profit?

A. 100          B. 300            C. 500

Problem 32 :

The quadrilateral shown below has vertices at (-8, 0), (-4, -4), (0, 8) and (4, 4).

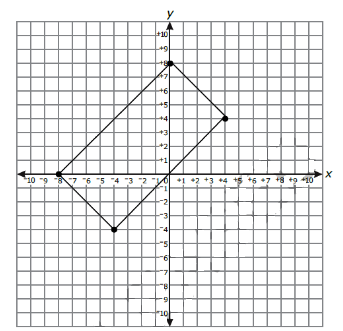
What is the area of the quadrilateral?

A. 32 units²      B. 45 units²          

C. 64 units²

Solution:

By using Pythagorean Theorem,

area of the quadrilateral = length × width

=  8√2 × 4√2

= 32(2)

= 64 units²

Problem 33 :

Which equation has a graph which is perpendicular to the line y = -2x and which passes through the point (-2, 3)?

A. x - 2y = 8          B. x + 2y = -8         C. x - 2y = -8

Solution:

The slope of the line that is perpendicular to y = -2x

m = 1/2

y = mx + b

Substitute (-2, 3) for (x, y) in above equation,

3 = (1/2)(-2) + b

3 = -1 + b

b = 4

y = (1/2)x + 4

2y = x + 8

x - 2y = -8

So, option (C) is correct.

Problem 34 :

The cost to mail a box of textbooks can be modeled by the function f(x) = 1.75x + 5.25, where x is the number of books mailed. What does the y-intercept of the function represent?

A. the cost to mail a box with no textbooks

B. the number of books mailed

C. the cost per book

Solution:

f(x) = 1.75x + 5.25

When x = 0,

f(x) = 1.75(0) + 5.25

= 0 + 5.25

f(x) = 5.25  (x = 0, no book)

5.25 is the y-intercept.

So, it represent the cost of mail a box with no text books.

So, option (A) is correct.

Problem 35 :

Which situation could be best modeled with an exponential function?

A. the value of a car that loses 6% of its value per year.

B. the cost to purchase different weights of bananas at a store.

C. the total number of miles run by a person who runs 8 miles per day.

Solution:

A.

Assuming the future value = P(1 - 6%)^t

it is exponential function.

C.

Total = 8 miles per day

It is linear function.

So, option (A) is correct.

Problem 36 :

The function f(x) = 4(2.0)^x models the population of rabbits on a farm after x months with no removal. The function g(x) = 2(2.0)^x models the number of rabbits removed from the population after x months. Which function, h(x), ,models the total number of rabbits on the farm after x months?

A. h(x) = 2(1.0)^x            B. h(x) = 2(2.0)^x       C. h(x) = 6(2.0)^x

Solution:

Given, f(x) = 4(2.0)^x

g(x) = 2(2.0)^x

h(x) = f(x) - g(x)

= 4(2.0)^x - 2(2.0)^x

= (2.0)^x[4 - 2]

h(x) = 2(2.0)^x

So, option (B) is correct.

Problem 37 :

Fred has $200. Each week he will save an additional $50. If Fred does not spend any of the money, how many weeks will it take for Fred to have $650?

A. 9            B. 13             C. 17

Solution:

50x + 200 = 650

50x = 650 - 200

50x = 450

x = 9

It will take 9 weeks.

So, option (A) is correct.

Problem 38 :

Solution:

So, option (B) is correct.

Problem 39 :

The table below shows the cost of a season ticket to an amusement park for various years.

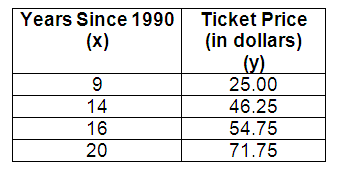
What is represented by the y-intercept of the line of best fit for this data set?

A. the predicted average change in ticket price per year.

B. the predicted number of years per $1 increase in ticket price.

C. the predicted price of a ticket in 1990.

Solution:

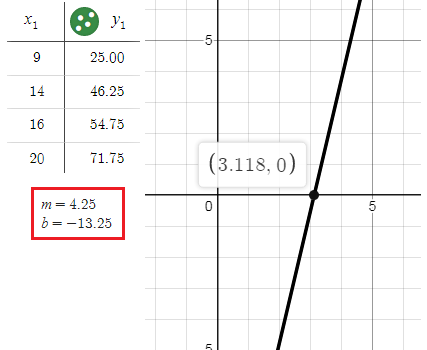
y = mx + b

y = 4.25x - 13.25

The predicted price of a ticket in 1990.

So, option (C) is correct.

Problem 40 :

Kerry wants to simplify the following:

Which of the following is the correct result?

A. 4x           B. 4x + 1          C. 20x²        D. 20x² + 1

Solution:

So, option (B) is correct.