MATCHING GRAPHS OF RECIPROCAL FUNCTIONS

• The graphs of most rational functions of the form 

f(x) = b / (cx + d) and f(x) = (ax + b)/(cx + d)

have both a vertical asymptote and horizontal asymptote

• You can determine the equation of vertical asymptote directly from the equation of the function by finding the zero of the denominator.
• You can determine the equation of the horizontal asymptote directly from the equation of the function by examining the ratio of the leading coefficients in the numerator and the denominator. This gives you the end behaviours of the
• function.
• To sketch the graph of a rational function, you can use the domain, intercepts, equations of asymptotes, and
• positive/negative intervals.

Rational functions of the form f(x) = b/(cx + d) have a vertical asymptote defined by x = -d/c and a horizontal asymptote defined by y = 0. Let us consider the example

f(x) = 2/(x - 3)

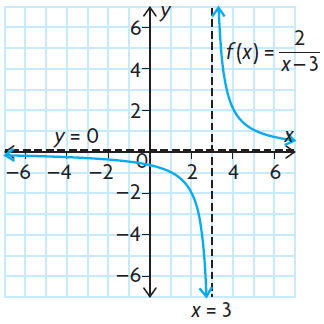
Most rational functions of the form f(x) = (ax + b)/(cx + d) have a vertical asymptote defined by x = -d/c and a horizontal asymptote defined by y = a/c. Let us consider the example

f(x) = (4x - 1)/(2x - 1)

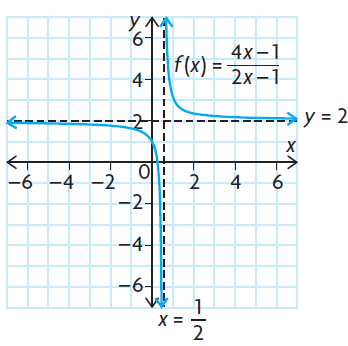
The exception occurs when the numerator and the denominator both contain a  common linear factor. This results in a graph of a horizontal line that has a hole where the zero of the common factor occurs. As a result, the graph has no asymptotes. For example, 

f(x) = (4x - 8)/(x - 2)

= 4(x - 2) / (x - 2)

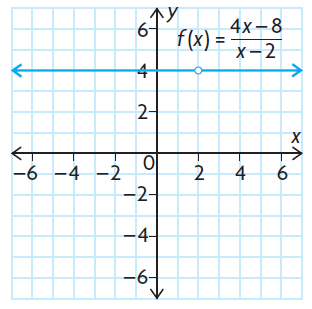
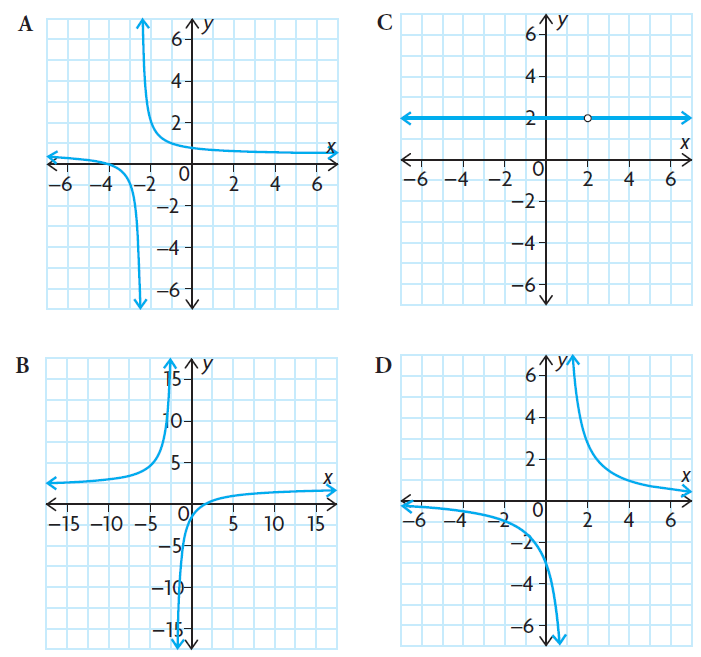
Problem 1 :

Match each function with its graph.

a) h(x) = (x + 4) / (2x + 5)

b) f(x) = 3/(x - 1)

c) m(x) = (2x -  4) / (x - 2)

d) g(x)= (2x - 3) / (x + 2)

Solution :

a) h(x) = (x + 4) / (2x + 5)

Finding the vertical asymptote :

By equating the denominator to 0, we get the equation of vertical asymptote.

2x + 5 = 0

x = -5/2

x = -2.5

So, vertical asymptote is at x = -2.5

Finding the horizontal asymptote :

Highest exponent of the numerator = 1

Highest exponent of the denominator = 1

Equation of horizontal asymptote y = Coefficient of number numerator / coefficient of denominator

y = 1/2

y = 0.5

Finding the hole :

Since there is no common factor in both numerator and denominator, there is no hole.

So, Graph A exactly matches these conditions.

b) f(x) = 3/(x - 1)

Solution :

Finding the vertical asymptote :

By equating the denominator to 0, we get the equation of vertical asymptote.

x - 1 = 0

x = 1

So, vertical asymptote is at x = 1

Finding the horizontal asymptote :

Highest exponent of the numerator = 0

Highest exponent of the denominator = 1

Highest exponent of numerator < highest exponent of denominator

So, equation of horizontal asymptote is x-axis or y = 0 

Finding the hole :

Since there is no common factor in both numerator and denominator, there is no hole.

So, Graph D exactly matches these conditions.

c) m(x) = (2x -  4) / (x - 2)

Solution :

Finding the vertical asymptote :

By equating the denominator to 0, we get the equation of vertical asymptote.

x - 2 = 0

x = 2

So, vertical asymptote is at x = 2

Finding the horizontal asymptote :

Highest exponent of the numerator = 1

Highest exponent of the denominator = 1

Equation of horizontal asymptote y = Coefficient of number numerator / coefficient of denominator

y = 2/1

y = 2

Finding the hole :

m(x) = (2x -  4) / (x - 2)

= 2(x - 2) / (x - 2)

m(x) = 2

So, there is hole at x = 2

So, Graph C exactly matches these conditions.

d) g(x) = (2x - 3) / (x + 2)

Finding the vertical asymptote :

By equating the denominator to 0, we get the equation of vertical asymptote.

x + 2 = 0

x = -2

So, vertical asymptote is at x = -2

Finding the horizontal asymptote :

Highest exponent of the numerator = 1

Highest exponent of the denominator = 1

Equation of horizontal asymptote y = Coefficient of number numerator / coefficient of denominator

y = 2/1

y = 2

Finding the hole :

Since there is no common factor in both numerator and denominator, there is no hole.

So, Graph B exactly matches these conditions.

Problem 2 :

Write an equation for a rational function with the properties as given.

a) a hole at x = 1

b) a vertical asymptote anywhere and a horizontal asymptote along the x-axis

c) a hole at x = -2 and a vertical asymptote at x = 1 

d) a vertical asymptote at x = 1and a horizontal asymptote at y = 2

e) an oblique asymptote, but no vertical asymptote

Solution :

a) a hole at x = 1

x - 1 is the factored form, since it is hole we should have this factor in both numerator and in denominator. Then the required function will be 

f(x) = 2 (x - 1) / (x - 1)

b) a vertical asymptote anywhere and a horizontal asymptote along the x-axis

Comparing the highest exponents of numerator and denominator, the denominator should be greater than the numerator.

1/x² - 4

Since the vertical asymptote may be anywhere we fix at x = -2 and x = 2.

c) a hole at x = -2 and a vertical asymptote at x = 1

f(x) = (x - 2) / (x + 1) (x - 2)

The common factor should be (x - 2) and vertical asymptote at x = 1, then (x + 1) must be the factor.

d) a vertical asymptote at x = 1and a horizontal asymptote at y = 2

f(x) = 2x/(x + 1)

e) an oblique asymptote, but no vertical asymptote

Since it doesn't have vertical asymptote while solving it, we will not get real value.

f(x) = x³ / (x² + 4)