MATCHING COEFFICIENTS OF POLYNOMIALS SAT QUESTIONS

Problem 1 :

If a ≠ 0, 

what is the value of x ?

a)  -5    b)  -1    c)  1   d)  5

Solution :

Doing cross multiplication, we get

5(x + a) = x(5 + a)

5x + 5a = 5x + xa

Equating the coefficient of a, we get

5 = x

So, the value of x is 5.

Problem 2 :

If x + k = 12 and p(x + k) = 36, what is the value of p ?

(A) 3     (B) 4     (C) 6    (D) 9     (E) 12

Solution :

x + k = 12 ------(1)

p(x + k) = 36 ------(2)

Applying the value of x + k = 12 in (2), we get

p(12) = 36

p = 36/12

p = 3

Problem 3 :

y = a(x - 2)(x + 4)

In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c, d) . Which of the following is equal to d ?

A) −9a     B) −8a     C) −5a      D) −2a

Solution :

y = a(x - 2)(x + 4)

Using distributive property, 

y = a(x² + 4x - 2x - 8)

y = a(x² + 2x - 8)

y = a(x² + 2 ⋅ x ⋅ 1 + 1² - 1² - 8)

y = a(x² + 2 ⋅ x ⋅ 1 + 1² - 1 - 8)

y = a[(x + 1)² - 9]

y = a(x + 1)² - 9a

Comparing with y = a(x - h)² + k

y = a(x - c)² + d

d = -9a

Problem 4 :

The equation

true for all values x ≠ 2/a, where a is the constant. What is the value of a ?

a)  -16      b)  -3      c)  3       d)  16

Solution :

Equating the coefficient of x², x and constants

-8a = 24  ------(1)

6 - 3a = 25  ------(2)

Continuing with (1), we get 

a = -24/8

a = -3

So, the value of a is -3.

Problem 5 :

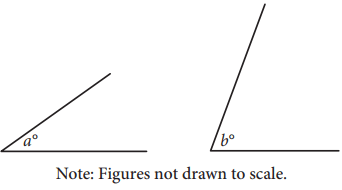
The angles shown above are acute and

sin(a°) = cos(b°)

If a = 4 − 22k and b = 6 − 13k, what is the value of k ?

Solution :

sin θ = cos (90 - θ)

Given,

sin(a°) = cos(b°)

sin(a°) = sin (90 - b°)

sin (4 - 22k) = sin (90 - (6 - 13k))

Equating angles, we get

4 - 22k = 90 - (6 - 13k))

4 - 22k = 90 - 6 + 13k

-22k - 13k = 84 - 4

-35k = 80

k = -80/35

k = -16/7

So, the value of k is -16/7.

Problem 6 :

In the xy-plane, the line determined by the points (2, k) and (k ,32) passes through the origin. Which of the following could be the value of k ?

A) 0      B) 4         C) 8         D) 16

Solution :

(2, k) and (k ,32)

Since the required line is passing through these two points, we can find slope of the line.

m = (y₂ - y₁) / (x₂ - x₁)

m = (32 - k) / (k - 2) ----(1)

Slope of the line passes through two points (2, k) and (0, 0)

m = (0 - k) / (0 - 2)

m = k/2 ----(2)

(1) = (2)

(32 - k) / (k - 2) = k/2

2(32 - k) = k(k - 2)

64 - 2k = k² - 2k

k² = 64

k = 8

Problem 7 :

tx + 12y = -3

The equation above is the equation of a line in the xy-plane, and t is a constant. If the slope of the line is 10, - what is the value of t ?

Solution :

tx + 12y = -3

12y = -tx - 3

y = -tx/12 - (3/12)

y = (-t/12)x - (1/4)

Slope of the line = 10

-t/12 = 10

-t = 10(12)

-t = 120

t = -120

So, the value of t is -120.

Problem 8 :

(-3x² + 5x - 2) - 2(x² - 2x - 1)

If the expression above is rewritten in the form ax² + bx + c, where a, b, and c are constants, what is the value of b ?

Solution :

= (-3x² + 5x - 2) - 2(x² - 2x - 1)

= -3x² + 5x - 2 - 2x² + 4x + 2

= -5x² + 9x

-5x² + 9x = ax² + bx + c

Comparing the corresponding terms,

a = -5, b = 9 and c = 0

So, the value of b is 9.

Problem 9 :

The perimeter of an equilateral triangle is 624 centimeters. The height of this triangle is k√3 centimeters, where k is a constant. What is the value of k?

Solution :

Perimeter of equilateral triangle = 624 centimeters

Let side length of the equilateral triangle be x

3x = 624

x = 624/3

x = 208

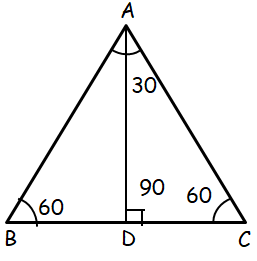
In triangle ADC,

AC = Hypotenuse = 208 = 2 (smaller side)

Let DC = Smaller side

2 DC = 208

DC = 208/2 ==> 104

AD = √3(Smaller side)

AD = √3(104)

AD = k√3

k = 104

So, the value of k is 104.

Problem 10 :

If a = 5√2 and 2a = √(2x), what is the value of x ?

Solution :

a = 5√2 and 2a = √(2x)

Applying the value of a, we get

2(5√2) = √(2x)

10√2 = √2 √x

√x = 10

Take square on both sides

x = 100