LINEAR EQUATIONS IN TWO VARIABLES BY GRAPHING

Solve each system by graphing. Show your answer both graphically and as an ordered pair.

Problem 1 :

y = x + 1

y = (-2/3)x – 4

Solution :

y = x + 1  ----(1)

y = (-2/3)x – 4  ----(2)

From (1), slope = 1 and y-intercept = 1

Slope = Rise / Run ==> 1/1

From y-intercept move 1 unit right and 1 unit up. Like this mark two more points and draw the line.

From (2), slope = -2/3 and y-intercept = -4

Slope = Rise / Run ==> -2/3

From y-intercept move 2 units left and 3 units up. Like this mark two more points and draw the line.

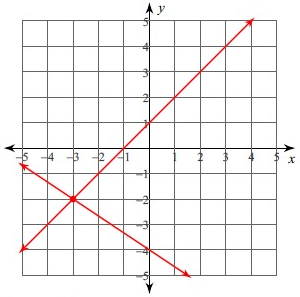
The point of intersection of these two lines is (-3, -2). So, the solution is (-3, -2).

Problem 2 :

y = -x – 4

y = x + 2

Solution :

y = -x – 4 -----(1)

y = x + 2 -----(2)

From (1), slope = -1 and y-intercept = -4

Slope = Rise / Run ==> -1/1

From y-intercept move 1 unit left  and 1 unit up. Like this mark two more points and draw the line.

From (2), slope = 1/1 and y-intercept = 2

Slope = Rise / Run ==> 1/1

From y-intercept move 1 unit left and 1 unit up. Like this mark two more points and draw the line.

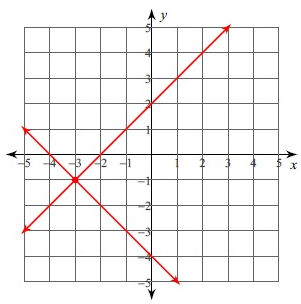
The point of intersection of these two lines is (-3, -1). So, the solution is (-3, -1).

Problem 3 :

x – y = 4

3x + y = 4

Solution :

x - y = 4

y = x - 4-----(1)

3x + y = 4

 y = -3x + 4-----(2)

From (1), slope = 1 and y-intercept = -4

Slope = Rise / Run ==> 1/1

From y-intercept move 1 unit right and 1 unit up. Like this mark two more points and draw the line.

From (2), slope = -3/1 and y-intercept = 4

Slope = Rise / Run ==> -3/1

From y-intercept move 3 units left and 1 unit up. Like this mark two more points and draw the line.

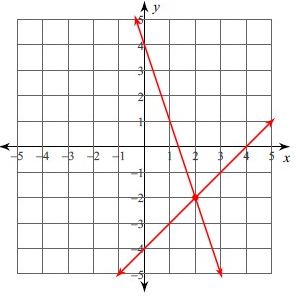
The point of intersection is (2, -2). So, the solution is (2, -2).

Problem 4 :

3x – 2y = 4

3x + 2y = 8

Solution :

3x - 2y = 4

2y = 3x - 4

y = (3/2) x - 2-----(1)

3x + 2y = 8

2y = -3x + 8

y = (-3/2)x + 4-----(2)

From (1), slope = 3/2 and y-intercept = -2

Slope = Rise / Run ==> 3/2

From y-intercept move 3 units left and 2 units up. Like this mark two more points and draw the line.

From (2), slope = -3/2 and y-intercept = 4

Slope = Rise / Run ==> -3/2

From y-intercept move 3 units left and 2 units up. Like this mark two more points and draw the line.

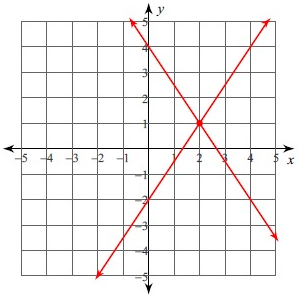
The point of intersection of these two lines is (2, 1). So, the solution (2, 1).