LENGTH OF THE MISSING SIDE OF 2D SHAPE FROM PERIMETER

Problem 1 :

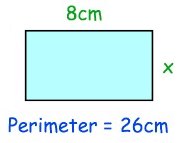
Solution :

Perimeter = 26 cm

Length = 8 cm

Perimeter of rectangle = 2l + 2w

26 = 2(8) + 2w

26 = 16 + 2w

2w = 26 - 16

2w = 10

w = 5 cm

The length of the missing side is 5 cm.

Problem 2 :

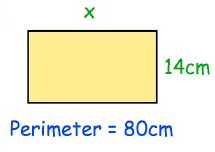
Solution :

Given, perimeter = 80 cm

Width = 14 cm

Perimeter of rectangle = 2l + 2w

80 = 2l + 2(14)

80 = 2l + 28

2l = 80 - 28

2l = 52

l = 52/2

l = 26 cm

The length of the missing side is 26 cm.

Problem 3 :

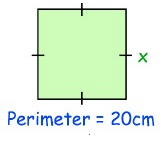
Solution :

Perimeter = 20 cm

Perimeter of square P = 4a

20 = 4a

a = 20/4

a = 5

The length of the missing side is 5 cm.

Problem 4 :

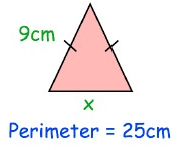
Solution :

Given, perimeter = 25 cm

Side a = 9 cm, b = 9 cm

Perimeter of triangle P = a + b + c

25 = 9 + 9 + c

25 = 18 + c

c = 25 - 18

c = 7 cm

The length of the missing side is 7 cm.

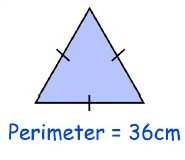
Problem 5:

Solution :

Perimeter = 36 cm

Perimeter of equilateral triangle P = 3 × a

36 = 3 × a

a = 36/3

a = 12 cm

The length of the missing side is 12 cm.

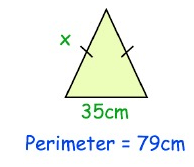
Problem 6 :

Solution :

Perimeter = 79 cm    

Side b = 35 cm

Perimeter of triangle P = 2a + b

79 = 2a + 35

2a = 79 - 35

2a = 44

a = 44/2

a = 22 cm

The length of the missing side is 22 cm.

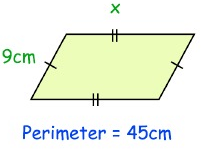
Problem 7 :

Solution :

Given, perimeter = 45 cm    

Width = 9 cm

Perimeter of rectangle P = 2(l + w)

45 = 2(l + 9)

45 = 2l + 18

2l = 45 - 18

2l = 27

l = 13.5 cm

The length of the missing side is 13.5 cm.

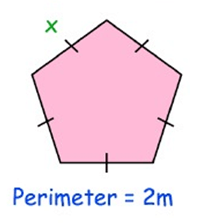
Problem 8:

Solution :

Given, perimeter = 2 m        

Perimeter of pentagon = 5 × a

2 = 5a

a = 2/5

a = 0.4 m

The length of the missing side is 0.4 m.

Problem 9 :

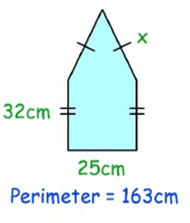
Solution :

Given, Perimeter = 163 cm

x + x + 32 + 32 + 25 = 163

2x + 89 = 163

2x = 163 - 89

2x = 74

x = 74/2

x = 37 cm

The length of the missing side is 37 cm.

Problem 10 :

If length and width of a rectangular is halved then its area will be _______

Solution :

Let l and w be the length and width of the rectangle.

After halved :

New length = l/2

Width = w/2

Area of new rectangle = length x width

= (l/2)(w/2)

= (1/4)(lw)

Area of new rectangle will be 1/4 of area of old rectangle.

Problem 11 :

The wire of length 84 m is converted into a square then broken to form a rectangle of length 30 m. Find the width of the rectangle.

Solution :

Length of wire = 84 m

Let w be the width of the rectangle.

length = 30 m

2(length + width) = 84

2(30 + w) = 84

30 + w = 84/2

30 + w = 42

w = 42 - 30

w = 12 m

So, the width of the rectangular shape is 12 m. 

Problem 12 :

The ratio of lengths of two rectangular fields is 4 : 3 and the ratio of their widths is 3 : 2. Find the ratio of their areas.

Solution :

Ratio between lengths = 4 : 3

Length first rectangle = 4l and second rectangle = 3l

Ratio between width = 3 : 2

Width of first rectangle = 3w, second rectangle = 2w

Ratio between area of rectangles :

= 4l(3w) : 3l(2w)

= 12lw : 6lw

= 12 : 6

= 2 : 1

Problem 13 :

The area of a square is 3/4 times area of a rectangle and width of the rectangle is 1/4 times of its length. Find the area of the square if the sum of length and width of the rectangle is 15 m.

Solution :

Let l be the length and w be the width.

Area of square = 3/4 x of area of rectangle

Width of the rectangle = 1/4 of length

length + width = 15

l + (1/4) l = 15

5l/4 = 15

l = 15(4/5)

l = 12 m

Width = (1/4) 12

= 3 m

Area of rectangle = 12(3)

= 36 square meter

Area of square = 3/4 of 36

= 3/4(36)

= 27 square meter

Problem 14 :

The length of the diagonal of a square is 50. Find the perimeter of a square.

Solution :

Length of diagonal = 50

Side length of square be x.

The diagonal will divide the square into right triangles.

x² + x² = 50

2x² = 50

x² = 50/2

x² = 25

x = 5

Perimeter of square = 4(side length)

= 4 (5)

= 20 units.