IS THERE AN ABSOLUTE MAXIMUM OR MINIMUM FOR EACH FUNCTION

How to check if the function has absolute maximum or minimum with using derivative ?

By comparing the degree and sign of leading coefficients, we find end behaviour of the polynomial function. This helps us to check if the function has absolute maximum or minimum.

Is there an absolute maximum or minimum for each function?

Problem 1 :

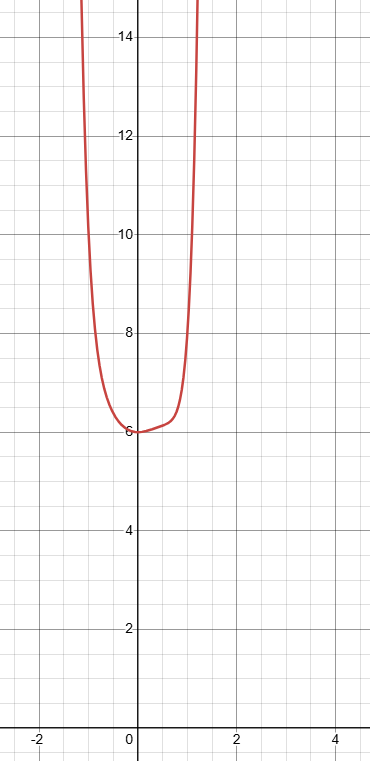
f(x) = 2x⁸ - x³ + x² + 6

Solution :

f(x) = 2x⁸ - x³ + x² + 6

Degree = 8 (even)

Sign of leading coefficient = 2 (positve)

Discussing end behaviour :

When x -> -∞ then f(x) --> ∞

When x --> ∞ then f(x) --> ∞

Since the degree is even and leading coefficient is positive based on end behaviour we know that the graphical form of the polynomial function opens up. So, the given function should have minimum.

Check using graphing calculator :

Problem 2 :

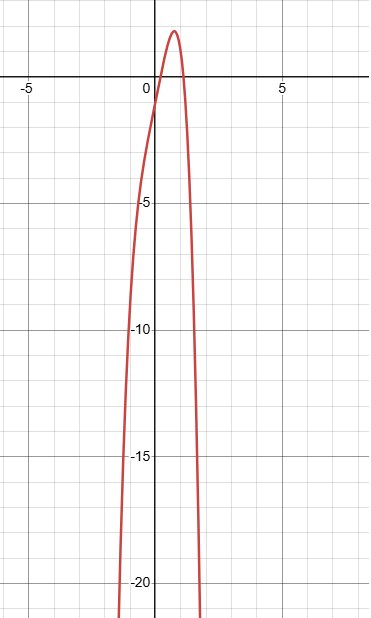
f(x) = -3x⁴ + 5x + 1

Solution :

f(x) = -3x⁴ + 5x + 1

Degree = 4 (even)

Sign of leading coefficient = -3 (negative)

Discussing end behaviour :

When x -> -∞ then f(x) --> -∞

When x --> ∞ then f(x) --> -∞

Since the degree is even and leading coefficient is negative based on end behaviour we know that the graphical form of the polynomial function opens down. So, the given function should have maximum.

Check using graphing calculator :

Problem 3 :

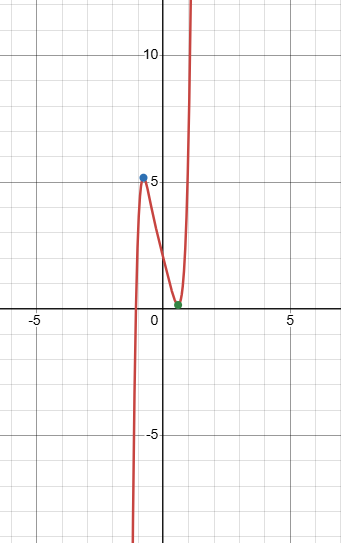
f(x) = 6x⁷ + 3x⁴ - 4x + 2

Solution :

f(x) = 6x⁷ + 3x⁴ - 4x + 2

Degree = 7 (odd)

Sign of leading coefficient = 6(positive)

Discussing end behaviour :

When x -> -∞ then f(x) --> -∞

When x --> ∞ then f(x) --> ∞

Since the degree is odd based on end behaviour, the function will not have nomaximum or minimum.

Check using graphing calculator :

Problem 4 :

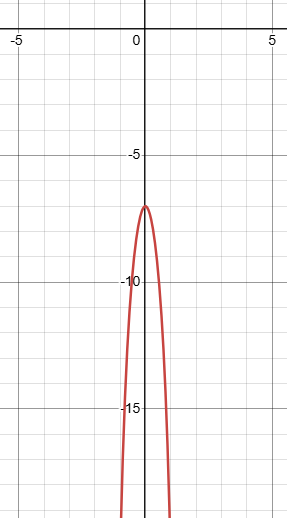
f(x) = -4x⁶ - 10x² - 7

Solution :

f(x) = -4x⁶ - 10x² - 7

Degree = 6 (even)

Sign of leading coefficient = -4 (negative)

Discussing end behaviour :

When x -> -∞ then f(x) --> -∞

When x --> ∞ then f(x) --> -∞

Since the degree is even and leading coefficient is negative based on end behaviour we know that the graphical form of the polynomial function opens down. So, the given function should have maximum.

Check using graphing calculator :

Problem 5 :

f(x) = -5x⁸ + 2x⁴ - 25

Solution :

f(x) = -5x⁸ + 2x⁴ - 25

Degree = 8 (even)

Sign of leading coefficient = -5 (negative)

Discussing end behaviour :

When x -> -∞ then f(x) --> -∞

When x --> ∞ then f(x) --> -∞

Since the degree is even and leading coefficient is negative based on end behaviour we know that the graphical form of the polynomial function opens down. So, the given function should have maximum.

Check using graphing calculator :

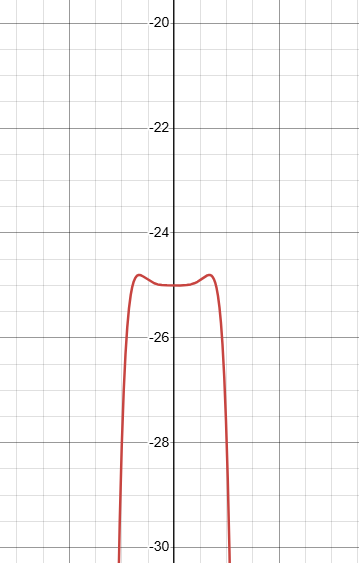
Problem 6 :

f(x) = 14x² + 1

Solution :

f(x) = 14x² + 1

Degree = 2 (even)

Sign of leading coefficient = 14 (positve)

Discussing end behaviour :

When x -> -∞ then f(x) --> ∞

When x --> ∞ then f(x) --> ∞

Since the degree is even and leading coefficient is positive based on end behaviour we know that the graphical form of the polynomial function opens up. So, the given function should have minimum.

Check using graphing calculator :

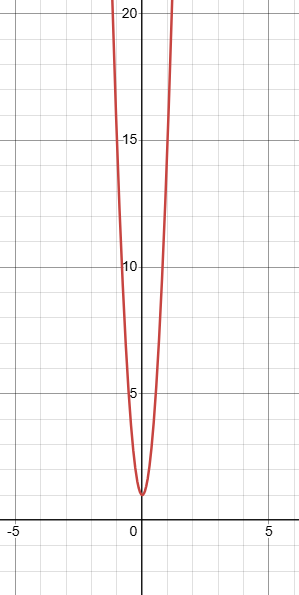
Problem 7 :

f(x) = -2x¹¹ - 5x⁶ + x²

Solution :

f(x) = -2x¹¹ - 5x⁶ + x²

Degree = 11 (odd)

Sign of leading coefficient = -2 (negative)

Discussing end behaviour :

When x -> -∞ then f(x) --> -∞

When x --> ∞ then f(x) --> ∞

Since the degree is odd based on end behaviour, the function will not have maximum or minimum.

Check using graphing calculator :

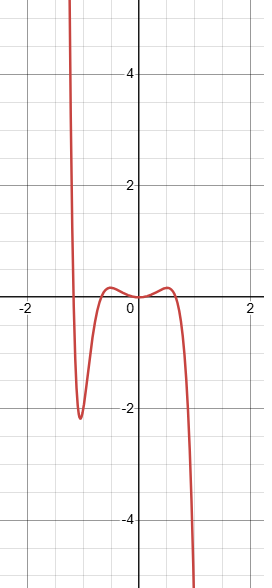
Problem 8 :

Give an example of a polynomial function that has each of the following end behaviours:

a)  As x--> -∞, y--> -∞ and as x--> ∞, y--> ∞

b)  As x--> ±∞, y--> ∞

c)  As x--> ±∞, y--> -∞

d) As x--> -∞, y--> ∞ and as x--> ∞, y--> -∞

Solution :

a)  As x--> -∞, y--> -∞ and as x--> ∞, y--> ∞

By analyzing the end behaviour, the required polynomial must have 

degree = odd

leading coefficient = positive or negative.

So, the required polynomial will be x³ + 2x² + 5.

b)  As x--> ±∞, y--> ∞

By analyzing the end behaviour, as x approaches positive or negative infinity, y will tend to positive infinity. The curve may opens up. It has the following properties,

degree = even

leading coefficient = positive

So, the required polynomial will be 2x⁴ - 5x³ + 1.

c)  As x--> ±∞, y--> -∞

By analyzing the end behaviour, as x approaches positive or negative infinity, y will tend to negativge infinity. The curve may opens down. It has the following properties,

degree = even

leading coefficient = negative

So, the required polynomial will be -3x⁴ - 4x³ - 2.

d) As x--> -∞, y--> ∞ and as x--> ∞, y--> -∞

By analyzing the end behaviour, the required polynomial must have 

degree = odd

leading coefficient = positive or negative.

So, the required polynomial will be -x³ + 2x² - 1.

Problem 9 :

a)  If a polynomial switches from increasing to decreasing, there will be a ____________, or _____________, ______________ output value.

b)  If a polynomial switches from decreasing to increasing, there will be a ____________, or _____________, ______________ output value.

Solution :

a)  If a polynomial switches from increasing to decreasing, there will be a relative  or local, maximum output value.

b)  If a polynomial switches from decreasing to increasing, there will be a relative or local, minimum output value.

Problem 10 :

If the polynomial has an even degree, there is either an absolute maximum or an absolute minimum.

Positive leading coefficient means you will have an absolute _______________

Negative leading coefficient means you will have an absolute _______________

Solution :

The polynomial function has even degree. When the polynomial function has absolute maximum, it should have positive leading coefficient.

When the polynomial function has absolute minimum, it should have negative leading coefficient.

• Positive leading coefficient means you will have an absolute maximum
• Negative leading coefficient means you will have an absolute minimum