INTERPRETING LINEAR FUNCTIONS WORD PROBLEMS WORKSHEET

Problem 1:

Charlie worked for a stone setting company this past summer. He earned $50 just for coming to work and an additional $30 every hour for each hour he worked. The linear function E(t) = 50 + 30t represents Charlie’s earnings E as a function of time worked t (in hours).

a)  Explain what E(4) represents.

b)  Find E(8). Explain what this represents in this problem.

c) Find E(5) - E(2).

Explain what this represents in this problem.

Solution

Problem 2 :

Kristen has $500 in her savings account. She is able to save $50 each month. The function S(m) = 50m + 500 represents the amount of money in her savings account S as a function of time in months m.

a) Find S(2). Explain what this represents in this problem.

b) Find m such that S(m)=800. Explain what this represents in this problem.

Solution

Problem 3 :

Luke is driving home from work. Let D(t) denote Luke’s remaining distance to drive D (measured in miles) after t minutes of driving.

What does the statement D(0) = 10 mean?

a) The drive between Luke’s home and his workplace takes 10 minutes.

b) The drive between Luke’s home and his workplace is 10 miles long.

c) Luke’s remaining distance is 0 miles after 10 minutes.

Solution

Problem 4 :

Ryan’s class had a math quiz where the grades were between 0 and 10. Let N(g) denote the number of students N whose grade on the exam was g.

What does the statement N(K) = 8 mean?

a) There are 8 students whose grade on the exam was K.

b) The value of the unknown K is equal to 8.

c) There are K students whose grade on the exam was 8.

Solution

Problem 5 :

Alicia went for a walk. Let D(t) denote the distance Alicia walked D (measures in miles) after walking for t hours.

What does the statement D(0.5) < D(1) - D(0.5) mean?

a) The distance Alicia has walked after walking for an hour is greater than the distance she has walked after half an hour.

b) The time it took Alicia to walk the first half mile is shorter than the time it took her to walk the following half mile.

c) The distance Alicia walked during the first half hour is shorter than the distance she walked during the following half hour.

Solution

Problem 1 :

The function below shows the cost of a hamburger with different numbers of toppings (t).

f(t) = 1.90 + 1.40t

a) What is the y-intercept, and what does it mean?

b) What is the slope, and what does it mean?

c) If Jodi paid $3.30 for a hamburger, how many toppings were on Jodi’s hamburger?

Solution

Problem 2 :

The function below shows the cost of an ice cream sundae with different numbers of toppings (t).

f(t) = 2.25 + 0.75t

a) What is the y-intercept, and what does it mean?

b) What is the slope, and what does it mean?

Solution

Problem 3 :

The graph below shows the number of newspapers delivered and total pay for Leona’ newspaper delivery job. What does the slope ? 

Solution

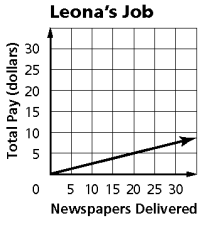
Problem 4 :

Dionne pays a fixed fee plus an hourly rate to rent a boat. The table below shows how much Dionne paid for the boat. What was Dionne’s hourly rate to rent the boat?

Solution

Problem 5 :

Colby put $100 in a savings account. The graph below shows  how the amount in the account would increase over the next ten years. What does the y-intercept represent? 

Solution

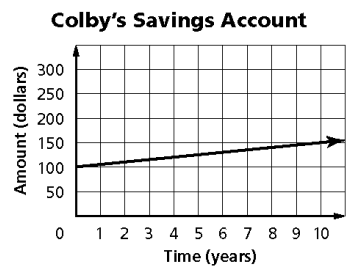
Problem 6 :

Tara pays a base rate for her long distance phone service plus a per-minute charge. The graph below shows what she would pay for her long distance phone service for the first 60 minutes. What does the y-intercept of this graph represent?

Solution

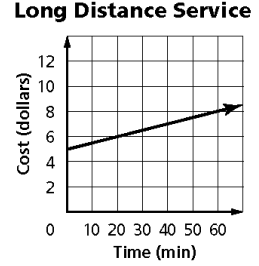
Problem 7 :

Rich is a member of a gym. He pays a monthly fee plus a per-visit fee. The equation below represents the monthly amount Rich pays for his membership to the gym per month for x visits.

y = 3x + 10

What does the y-intercept of the graph of this equation represent?

Solution