INTERPRETING LINEAR EQUATION WORD PROBLEMS

Problem 1 :

The total cost y (in dollars) of a gym membership after x months is given by

y = 45x + 75.

What is the total cost of the membership after 9 months?

Solution :

x = number of month, y = total cost 

Total cost of membership after 9 months :

When x = 9

y = 45(9) + 75

y = 405 + 75

y = 480

So, $480 is the amount for membership after 9 months.

Problem 2 :

Your annual membership fee to a nature society lets you camp at several campgrounds. Your total annual cost y (in dollars) to use the campgrounds is given by

y = 5x + 35

where x is the number of nights you camp. What do the slope and y-intercept represent?

Solution :

y = 5x + 35

x = number of nights you camp, y = annual cost

Comparing the given equation with y = mx + b, we get

the slope is 5, so cost spent per night is $5.

y-intercept = 35

So, the membership fee is $35 per year.

Problem 3 :

Bowling alleys often charge a fixed fee to rent shoes and then charge for each game you bowl. The function

C(g) = 3g + 1.5

gives the total cost C (in dollars) to bowl g games. What is the cost to rent shoes? What is the cost per game?

Solution :

C(g) = 3g + 1.5

Here slope (m) = 3 and y-intercept (b) = 1.5

Cost to rent shoes = 1.5

Cost per game = 3

Problem 4 :

You purchase a 300 minute phone card. The function

M(w) = -30w + 300

models the number M of minutes that remain on the card after w weeks. Describe how to determine a reasonable domain and range. Graph the function. How many minutes per week do you use the card?

Solution :

Let us find, x and y-intercepts to fix domain and range.

x-axis represents number of weeks and y-axis represents number of minutes. x and y-intercepts are (0, 300) and (10, 0).

Problem 5 :

An honor society has $150 to buy science museum and art museum tickets for student awards. The numbers of tickets that can be bought are given by 5s + 7a = 150 where s is the number of science museum tickets (at $5 each) and a is the number of art museum tickets (at $7 each). Graph the equation.

Solution :

Problem 6 :

l = 24 + 3.5 m

One end of a spring is attached to a ceiling. When an object of mass m kilograms is attached to the other end of the spring, the spring stretches to a length of  l centimeters as shown in the equation above. What is m when l is 73 ?

a) 14     b) 27.7      c) 73       d) 279.5

Solution :

l = 24 + 3.5 m

When l = 73

73 = 24 + 3.5m

73 - 24 = 3.5m

3.5m = 49

m = 49/3.5

m = 14

So, option a is correct.

Problem 7 :

The cost of parking in a parking garage in Chicago is represented by the equation

y = 15x + 20

where y is the total cost (in dollars) and x is the time (in hours). The table shows the total cost to park in a parking garage in Denver. Which city’s parking garage charges more per hour and by how much more? After how many hours would parking in both cities cost the same?

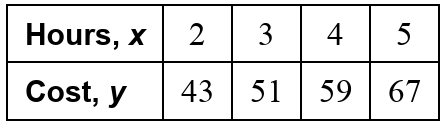
Solution :

The cost of parking in a parking garage in Chicago :

y = 15x + 20

Cost per hour in Chicago = 15

The cost of parking parking garage in Denver :

y = mx + b

Slope : 

(2, 43) and (3, 51)

= (51 - 43)/(3 - 2)

= 8/1

Sloep (m) = 8

y = 8x + b

applying the point (4, 59), we get

59 = 8(4) + b

59 = 32 + b

b = 59 - 32

b = 27

y = 8x + 27

Cost per hour in Denver = 8

Cost per hour in Chicago is greater, by 15 - 8. That is $7 greater.

y = y

15x + 20 = 8x + 27

15x - 8x = 27 - 20

7x = 7

x = 1

For 1 hour, its costs is the same.