INTERPRETING INEQUALITIES IN ONE VARIABLE

Describe and graph the interval of real numbers for the inequality.

Problem 1 :

x < 3

Solution :

The value of x should be less than 3. So, in the number line we will shade to the left of 3 upto infinity.

Since we have less than sign, we use open circle.

Problem 2 :

-1 < x ≤ 4

Solution :

The value of x should be in between -1 and 4. Here 1 cannot be included as a solution, because we have less than sign.

Since we have less than sign near 1, we have to use open circle for 1.

We have less than or equal sign near 4, so we use filled circle for 4.

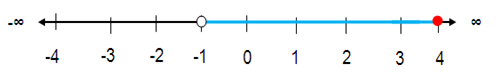
Describe and graph the interval of real numbers.

Problem 3 :

x ≤ 2

Solution :

The values of x should be less than or equal to 2. We can accept 2 and lesser than 2 as solution. So, we have to shade left of 2 upto -infinity.

Problem 4 :

-2 ≤ x < 5

Solution :

The values of x should be in between -2 and 5. We can accept -2 and cannot accept 5. So, we have to shade between -2 and 5 and -2 with filled circle and 5 with unfilled circle.

Convert the interval notation to graph.

Problem 5 :

(-∞, 7)

Solution :

x < 7

The interval notation clearly shows which side to be shaded.

Problem 6 :

[-3, 3]

Solution :

The solution is in between -3 to 3. For both -3 and 3, we have to use the closed bracket.

Problem 7 :

x is negative.

Solution :

Since the solution is negative, we shade the negative side of the number line.

Problem 8 :

x is greater than or equal to 2 and less than or equal to 6.

Solution :

x ≥ 2 and x ≤ 6

Use interval notation to describe the interval of real numbers.

Problem 9 :

x > -3

Solution :

Since the solution should be greater than -3, we shade right of -3.

Problem 10 :

-7 < x < -2

Solution :

The solution is in between -7 and -2. We cannot include -7 and -2 because we have less than sign.

Convert the shaded region into inequality.

Problem 11 :

Solution :

[-2, 1]

Problem 12 :

Solution :

 The shaded part right of -1 and near -1 we have closed bracket. So, the inequality is  x ≥ -1

Problem 13 :

x is greater than -3 and less than or equal to 4.

Solution :

x > -3  and x ≤ 4

The solution should be in between -3 and 4. Near -3 we have greater than sign, so use open bracket. Near 4

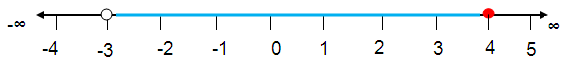
Problem 14 :

x is positive.

Solution :

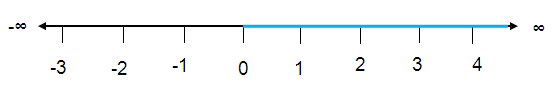
Convert the given inequality into other forms.

Problem 15 :

4 < x ≤ 9

Solution :

Graph :

Inequality :

(4, 9]

Problem 16 :

 x ≥ -1

Solution :

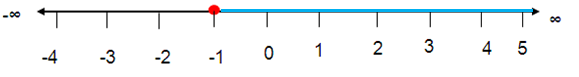
Inequality :

[-1, ∞)

Problem 17 :

[-3, ∞)

Solution :

Inequality :

x ≤ -3

Graph :

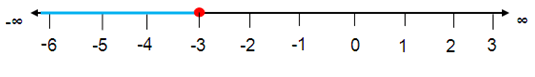
Problem 18 :

(-5, 7)

Solution :

-5 < x < 7

Problem 19 :

Solution :

Inequality :

-1 < x < ∞

Interval :

(-1, ∞)

Problem 20 :

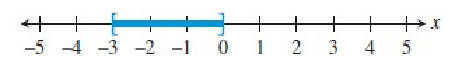
Solution :

Inequality :

-3 < x < 0

Interval :

(-3, 0)