INTERIOR ANGLES OF A QUADRILATERAL

Find the value of x in the following quadrilaterals :

Problem 1 :

Solution :

Sum of interior angles of a quadrilateral = 360

x + 110 + 105 + 80 = 360

x + 295 = 360

Subtracting 295 on both sides.

x = 360 - 295

x = 65

Problem 2 :

Solution :

x + 56 + 121 + 90 = 360

x + 267 = 360

Subtracting 267 on both sides.

x = 360 - 267

x = 93

Problem 3 :

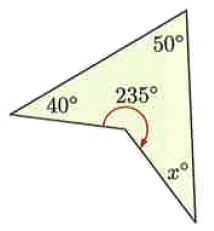
Solution :

40 + 235 + x + 50 = 360

325 + x = 360

Subtracting 325 on both sides.

x = 360 - 325

x = 35

Problem 4 :

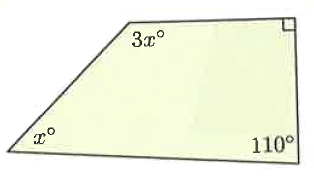
Solution :

x + 3x + 110 + 90 = 360

4x + 200 = 360

Subtracting 200 on both sides.

4x = 360 - 200

4x = 160

Dividing by 4 on both sides.

x = 160/4

x = 40

Problem 5 :

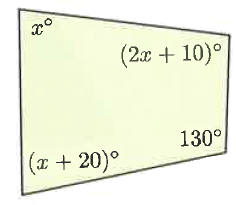
Solution :

x + 20 + 130 + 2x + 10 + x = 360

4x + 160 = 360

Subtracting 160 on both sides.

4x = 360 - 160

4x = 200

Dividing by 4 on both sides.

x = 200/4

x = 50

Problem 6 :

Find the values of a and b.

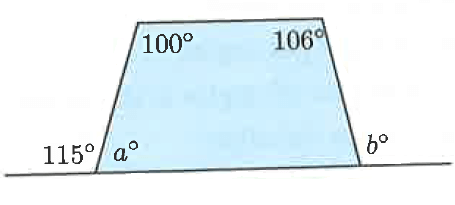
Solution :

115 + a = 180

Subtracting 115 on both sides.

a = 180 - 115

a = 65

Sum of interior angles of a quadrilateral = 360

a + 100 + 106 + b = 360

65 + 100 + 106 + b = 360

271 + b = 360

Subtracting 271 on both sides.

b = 360 - 271

b = 89

Problem 7 :

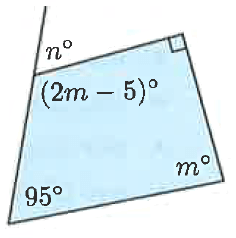
Solution :

Sum of interior angles of a quadrilateral = 360

m + 95 + 2m - 5 + 90 = 360

3m + 90 + 90 = 360

3m + 180 = 360

Subtracting 180 on both sides.

3m = 360 - 180

3m = 180

Dividing by 3 on both sides.

m = 180/3

m = 60

2m - 5 and n are linear pair.

2m - 5 + n = 180

2(60) - 5 + n = 180

120 - 5 + n = 180

115 + n = 180

Subtracting 115 on both sides.

n = 180 - 115

n = 65

Problem 8 :

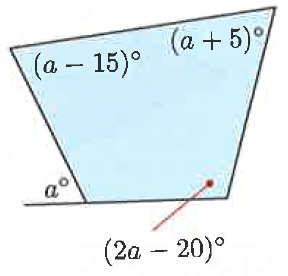
Solution :

a - 15 + a + 5 + 2a - 20 + 180 - a = 360

3a - 15 - 20 + 5 + 180 = 360

3a + 150 = 360

Subtracting 150 on both sides.

3a = 360 - 150

3a = 210

Dividing by 3 on both sides.

a = 210/3

a = 70

Problem 9 :

find the measures of the numbered angles in rhombus DEFG.

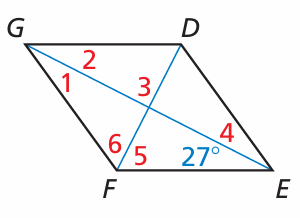
Solution :

Since it is rhombus all four sides will be equal, diagonals will be equal and diagonals will be perpendicular and bisect each other.

∠3 = 90

Let H be the point of intersection of two diagonals.

In triangle FEH,

∠5 + 27 + 90 = 180

∠5 + 117 = 180

∠5 = 180 - 117

∠5 = 63

∠2 = 27 (alternate interior angles)

In triangle HGD,

∠FDG = 63 (alternate interior angles)

∠FDE = 63

∠6 = 63

∠4 = ∠1 = 27

Problem 10 :

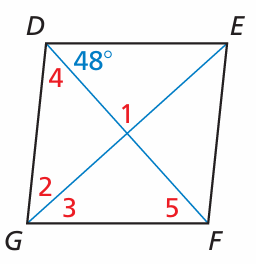
Solution :

∠1 = 90

∠5 = 48 (alternate interior angles)

∠4 = 48 (bisecting angle)

∠2 + ∠3 + ∠5 + ∠4 = 180

∠2 + ∠2 + 48 + 48 = 180

2∠2 + 96 = 180

2∠2 = 180 - 96

2∠2 = 84

∠2 = 84/2

∠2 = 42

∠3 = 42

Problem 11 :

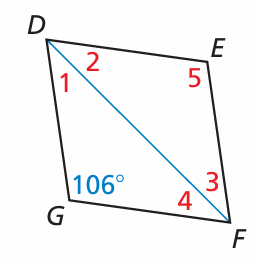
Solution :

∠1 = ∠4 (DG and GF are equal)

∠1 + 106 + ∠4 = 180

2∠1 = 180 - 106

2∠1 = 74

∠1 = 74/2

∠1 = 37

∠4 = 37

∠4 = ∠3 = 37 = ∠2

∠5 = 106 

Problem 12 :

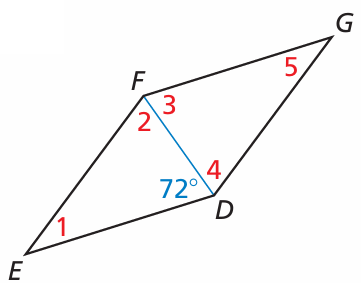
Solution :

∠2 = 72

∠3 = 72 and ∠4 = 72

In triangle EFD,

∠1 + ∠2 + 72 = 180

2∠1 = 180 - 72

2∠1 = 108

∠1 = 108/2

∠1 = 54

∠5 = 54

Problem 13 :

The measures of the interior angles of a quadrilateral are x°, 3x°, 5x°, and 7x°. Find the measures of all the interior angles.

Solution :

Sum of interior angles in a quadrilateral = 360

x + 3x + 5x + 7x = 360

16x = 360

x = 360/16

x = 22.5

3x ==> 3(22.5) ==> 67.5

5x ==> 5(22.5) ==> 112.5

7x ==> 7(22.5) ==> 157.5

So, the required interior angles are 22.5, 67.5, 112.5 and 157.5

Problem 14 :

Find the values of x and y that make the quadrilateral a parallelogram

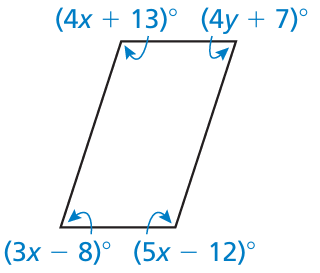
Solution :

Sum of co-interior angles = 180

3x - 8 + 4x + 13 = 180

7x + 5 = 180

7x = 180 - 5

7x = 175

x = 175/7

x = 25

5x - 12 + 4y + 7 = 180

5(25) - 12 + 4y + 7 = 180

125 - 12 + 7 + 4y = 180

4y = 180 - 120

4y = 60

y = 60/4

y = 15

So, the value of x is 25 and y is 25.