ORDER THE SIDE LENGTHS OF THE TRIANGLE FROM SHORTEST TO LONGEST

Problem 1 :

For which measures of the sides of ABC is angle B the largest angle of the triangle?

a) AB = 2, BC = 6, AC = 7

b) AB = 6, BC = 12, AC = 8

c) AB = 16, BC = 9, AC = 10

d) AB = 18, BC = 14, AC = 5

Solution :

In triangle ABC,

• AB is the side which is opposite to ∠C
• AC is the side which is opposite to ∠B
• BC is the side which is opposite to ∠A

a) AB = 2, BC = 6, AC = 7

Ordering sides from least to greatest :

AB < BC < AC

Ordering angles from least to greatest :

∠C < ∠A < ∠B

Here ∠B is the largest, so option a is correct.

Problem 2 :

As shown in the diagram of ACD below, B is a point on AC and DB is drawn.

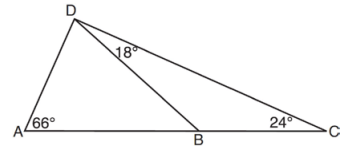
If m∠A = 66, m∠CDB = 18, and m∠C = 24, what is the longest side of ABD?

a) AB        b) DC      c) AD      d) BD

Solution :

In triangle BCD,

m∠CBD = 180 - (18 + 24)

m∠CBD = 180 - 42

m∠CBD = 138

In triangle ABD,

m∠DBA = 180 - 138

m∠DBA = 42

m∠ADB = 180 - (42 + 66)

m∠ADB = 180 - 108

m∠ADB = 72

In triangle ADB, m∠ADB is the largest. So, AB is the largest side.

Problem 3 :

In CAT, m∠C = 65, m∠A = 40, and B is a point on side CA, such that TB ⊥ CA. Which line segment is shortest ?

a) CT     b) BC      c) TB       d) AT

Solution :

Drawing the picture from the given details.

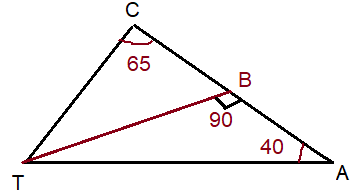
In triangle TAB,

∠BTA = 180 - (90 + 40)

∠BTA = 180 - 130

∠BTA = 50

In triangle CTB

∠CTB = 180 - (65 + 90)

∠CTB = 180 - 155

∠CTB = 25

∠CTA = ∠CTB + ∠BTA

∠CTA = 25 + 50

∠CTA = 75

Smallest angle measure in triangle CTA is ∠TAC. So, CT is the shortest side.

Problem 4 :

In the diagram of quadrilateral NAVY below, m∠YNA = 30°, m∠YAN = 38°, m∠AVY = 94°, and m∠VAY = 46°.

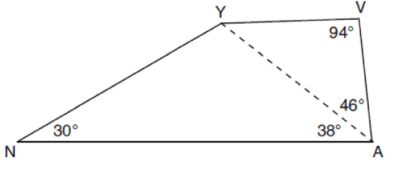
Which segment has the shortest length?

a) AY      b) NY     c) VA       d) VY

Solution :

In triangle VAY,

m∠VYA = 180 - (94+46)

= 180 - 140

m∠VYA = 40

In triangle YAN,

m∠NYA = 180 - (30+38)

= 180 - 68

m∠NYA = 112

m∠NYA + m∠AYV = 112 + 40

m∠NYV = 152

m∠NAV = 38 + 46

m∠NAV = 84

38° is the shortest angle measure, then NY is the shortest side.

Problem 5 :

In the diagram below of ABC with side AC extended through D, m∠A = 37 and m∠BCD = 117. Which side of ABC is the longest side? Justify your answer.

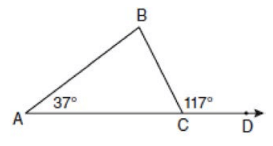
Solution :

m∠BCD = 117

m∠ACB = 180 - 117

m∠ACB = 63

m∠ABC = 180 - (63 + 37)

m∠ABC = 80°

The largest angle measure is 80°, so the longest side is AC.

Problem 6 :

As shown in the diagram below, AS is a diagonal of trapezoid STAR, RA||ST, m∠ATS = 48, m∠RSA = 47, and m∠ARS = 68

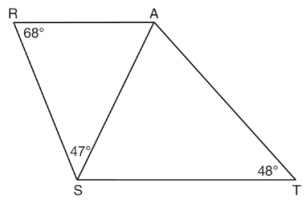
Determine and state the longest side of SAT.

Solution :

In triangle RAS,

m∠RAS = 180 - (68 + 47)

m∠RAS = 180 - 115

m∠RAS = 65

m∠AST = 65 (alternate interior angles)

In triangle AST,

m∠SAT = 180 - 65 - 48

m∠SAT = 67

67° is the largest angle measure, then ST is the largest side.

Problem 7 :

In ABC, m∠A = x² + 12, m∠B = 11x + 5, and m∠C = 13x − 17. Determine the longest side of ABC

Solution :

In triangle ABC,

m∠A + m∠B + m∠C = 180

x² + 12 + 11x + 5 + 13x − 17 = 180

x² + 24x + 17 - 17 = 180

x² + 24x - 180 = 0

(x - 6)(x + 30) = 0

x = 6 and x = -30

So, AC is the longest side.