IDENTIFYING SLOPE AND Y INTERCEPT FROM EQUATION

Solve each for y, identify m and y – intercept and graph each.

Problem 1 :

2y = 4x - 8

Solution :

Given, 2y = 4x - 8

The given equation is in standard form, to find slope we have to convert it into slope intercept form is y = mx + b.

y = (4/2)x – 8/2

y = 2x – 4

Comparing with y = mx + b

m = 2

So, 2 is slope and y – intercept is -4.

Problem 2 :

2x - y = -8

Solution :

Given, 2x – y = - 8

The given equation is in standard form, to find slope we have to convert it into slope intercept form is y = mx + b.

-y = -2x – 8

y = 2x + 8

So, 2 is slope and y – intercept = 8

Problem 3 :

-4x + 3y = -9

Solution :

-4x + 3y = -9

The given equation is in standard form, to find slope we have to convert it into slope intercept form is y = mx + b.

3y = 4x – 9

y = (4/3)x – 9/3

y = (4/3)x - 3

m = 4/3

So, 4/3 is slope and y – intercept = -3

Problem 4 :

6 - 2y = 5x

Solution :

Standard form : 6 – 2y = 5x

-2y = 5x + 6

-y = (5/2)x + 6/2

-y = (5/2)x + 3

y = (-5/2)x - 3

So, -5/2 is slope and y- intercept = -3

Problem 5 :

 5y = -15

Solution :

5y = -15

Dividing by 5 on both sides, we get

y = -15/5

y = -3

y = 0x - 3

So, slope is 0 and y- intercept is -3.

Problem 6 :

-2x = 4

Solution :

-2x = 4

Dividing by -2 on both sides, we get x = -2.

So, slope is 2 and y- intercept is 4.

Problem 7 :

You decide to rent tables from a different company. The situation can be modeled by the equation 4x + 6y = 180, where x is the number of small tables and y is the number of large tables. Graph the equation and interpret the intercepts.

Solution :

4x + 6y = 180

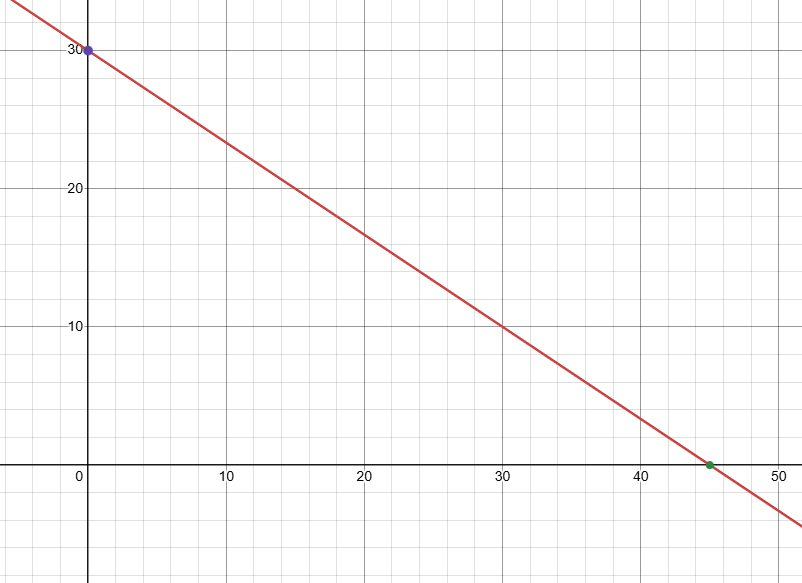
When there is no small tables there, it must be 45 large tables.

When there is no large tables there, it must be 30 small tables.

Problem 8 :

The function c(x) = 9 + 1.50x represents the total cost (in dollars) of a large pizza, where x is the number of additional toppings. Find the zero of the function. Does the zero make sense in this situation? Explain.?

Solution :

c(x) = 9 + 1.50x

To find the zero of this fucntion, we will put c(x) = 0

9 + 1.50 x = 0

1.50x = -9

x = -9/1.50

x = -6

The zero of the function is -6 . This zero does not make sense in the context of the problem because the number of additional toppings cannot be negative, and the cost of a pizza cannot be $0.

Problem 9 :

Consider the equation 8 = 4x + 16. Write a function so that the solution of the equation is the zero of the function. Explain your reasoning.

Solution :

Let us solve the given equation

8 = 4x + 16

8 - 16 = 4x

4x = -8

x = -8/4

x = -2

-2 is the zero of the function.

To make -2 as zero of the function, we should have the function f(x) = 4x + 8.

Problem 10 :

A football team has an away game, and the bus breaks down. The coaches decide to drive the players to the game in cars and vans. Four players can ride in each car. Six players can ride in each van. There are 48 players on the team. The equation 4x + 6y = 48 models this situation, where x is the number of cars and y is the number of vans. 

a. Graph the equation. Interpret the intercepts.

b. Find two possible solutions in the context of the problem.

Solution :

4x + 6y = 48

a)

Finding x and y - intercepts :

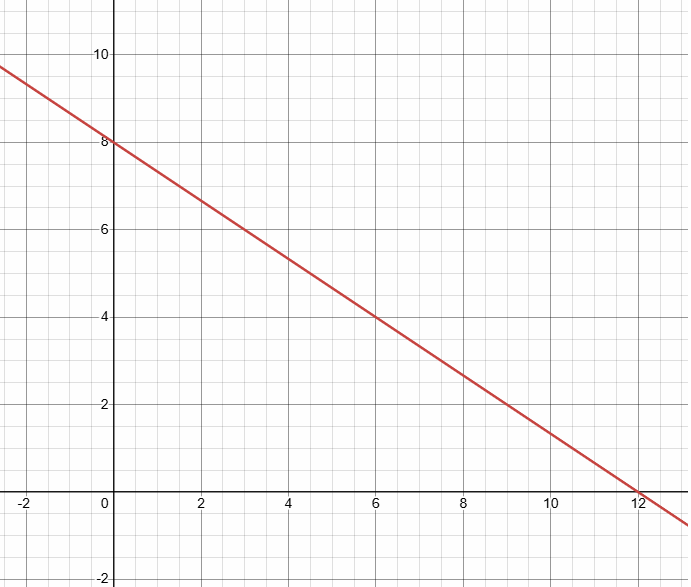
• When number of cars is 8, number of vans will be 0.
• When number of cars is 12, number of cars will be 0.

b)  4x + 6y = 48

The solutions are (1, 7) and (3, 6).