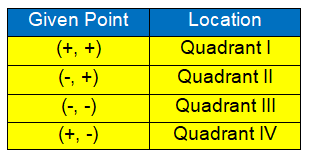
IDENTIFYING QUADRANT OF THE COORDINATE POINT LIES

By table,

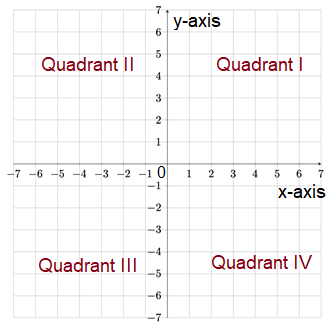
By graph,

Example 1 :

Describe the location of the point.

Solution :

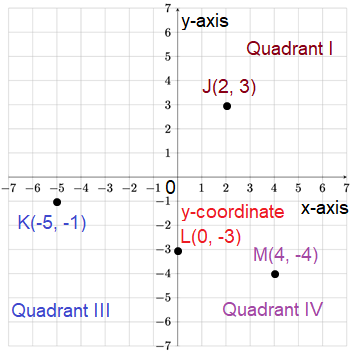
By observing the above graph,

(i)  J(2, 3) is located at Quadrant I.

(ii)   K(-5, -1) is located at Quadrant III.

(iii)  L(0, -3) is located at y-coordinate.

(iv)  M(4, -4) is located at Quadrant IV.

Example 2 :

What is the x-coordinate of the point (-12, 7)? What is the y-coordinate?

Solution :

The x-coordinate of the point is -12. 

The y-coordinate of the point is 7.

Example 3 :

A point has one positive coordinate and one negative coordinate. Can you determine in which quadrant the point lies? Explain.

Solution :

If the point has one positive coordinate and one negative coordinate that is located at Quadrant IV.

Example 4 :

Give the coordinates of the point.

Solution :

By observing the above graph,

The coordinates of Point A are (-4, 2).

The coordinates of Point B are (0, 3).

The coordinates of Point C are (0, 0).

The coordinates of Point D are (4, 0).

The coordinates of Point E are (-2, -4).

The coordinates of Point F are (3, 3).

The coordinates of Point G are (4, 4).

The coordinates of Point H are (-3, -2).

Example 5 :

Use the variable expression 2x + 1.

a)  Evaluate the expression when x = -3, -2, -1, 0, 1, 2, and 3

b)  Use your results from part (a) to write a list of ordered pairs in the form (x, 2x + 1).

Solution :

a)

Given, expression 2x + 1

b)

write a list of ordered pairs in the form (x, 2x + 1)

From (a),

Example 6 :

A blizzard hits a town at midnight. The table shows the hourly temperatures from midnight to 8:00 A.M.

a)  Display the data in a line graph.

b)  Make three observations from the graph.

Solution :

a)  Write the ordered pairs. (0, 7) (3, 0) (1, 5) (4, –1) (2, 3) (5, −4) (6, −5) (7, −2) (8, 2) Plot and label the ordered pairs. Then connect the ordered pairs with line segments.

b)  

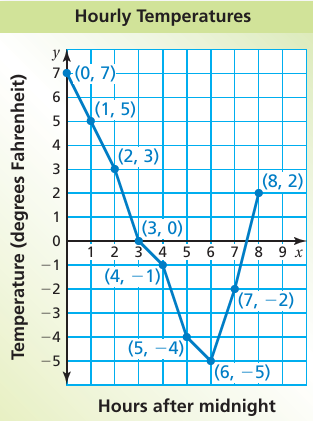
Three possible observations follow:

● The hourly temperatures decrease from midnight to 6:00 a.m.

● The hourly temperatures increase from 6:00 a.m. to 8:00 a.m.

● The greatest decrease in hourly temperatures from one hour to the next is 3°F. This happens twice: from 2:00 a.m. to 3:00 a.m. and from 4:00 a.m. to 5:00 a.m.

Example 7 :

How many quadrants are in a coordinate plane?

Solution :

There are four quadrants.

Example 8 :

Is the point (0, −7) on the x-axis or the y-axis?

Solution :

When the input is 0, the point is on the y-axis.

Example 9 :

Which point does not belong with the other three? Explain your reasoning. (−2, 1) (−4, 5) (2, −3) (−1, 3)

Solution :

The points in the coordinate plane will be in the form :

So, the point (2, -3) is not belongs to the group.

Example 10 :

Describe the possible location(s) of the point (x, y).

a) x > 0, y > 0

b) x < 0, y < 0

c) x > 0, y < 0

d)  x > 0

e)  y < 0

f) x = 0, y = 0

Solution :

a) x > 0, y > 0

The point will be in the form (x, y). So, the required point will be in the first quadrant.

b) x < 0, y < 0

The point will be in the form (-x, -y). So, the required point will be in the third  quadrant.

c) x > 0, y < 0

The point will be in the form (x, -y). So, the required point will be in the fourth  quadrant.

d)  x > 0

The point will be in the forms (x, y) or (x, -y). So, the required point will be in the first quadrant or fourth quadrants.

e)  y < 0

The point will be in the form (x, -y) or (-x, -y). So, the required point will be in the first quadrant and third quadrants,

f) x = 0, y = 0

The point (0, 0) is at orgin.