IDENTIFYING DIRECT ANG INVERSE VARIATION FROM TABLE

Direct variation :

Two variables x and y show direct variation when

y = ax

for some nonzero constant a.

Another type of variation is called inverse variation.

Inverse variation :

Two variables x and y show inverse variation when they are related as follows:

y = a/x, a ≠ 0

The constant a is the constant of variation, and y is said to vary inversely with x.

Tell whether x and y show direct variation, inverse variation, or neither.

Problem 1 :

Solution :

Finding the product of x and y :

x = 2

y = -12

xy = -24

x = 4

y = -6

xy = -24

x = 6

y = -4

xy = -24

x = 8

y = -3

xy = -24

The product of x and y is constant.

Finding the ratio of y t ox :

x = 2

y = -12

y/x = -6

x = 4

y = -6

y/x = -3/2

x = 6

y = -4

y/x = -2/3

x = 8

y = -3

xy = -3/8

The ratio is not a constant. So, the given table represents the direct variation.

Problem 2 :

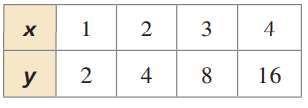
Solution :

Finding the product of x and y :

x = 1

y = 2

xy = 2

x = 2

y = 4

xy = 8

x = 3

y = 8

xy = 24

x = 4

y = 16

xy = 64

The product of x and y is not constant.

Finding the ratio of y t ox :

x = 1

y = 2

y/x = 2

x = 2

y = 4

y/x = 2

x = 3

y = 8

y/x = 8/3

x = 4

y = 16

y/x = 4

The ratio of y to x is not constant. So, the table represents the neither relationship.

Problem 3 :

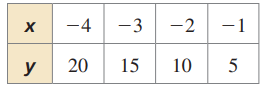
Solution :

Finding the product of x and y :

x = -4

y = 20

xy = -80

x = -3

y = 15

y/x = -45

x = -2

y = 10

y/x = -20

x = -1

y = 5

y/x = -5

The product of x and y is not a constant.

Finding the ratio of y to x :

x = -4

y = 20

y/x = -5

x = -3

y = 15

y/x = -5

x = -2

y = 10

y/x = -5

x = -1

y = 5

y/x = -5

The ratio between y to x is constant. So, the table represents inverse variation.

Problem 4 :

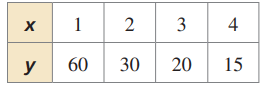
Solution :

Finding the product of x and y :

x = 1

y = 60

xy = 60

x = 2

y = 30

xy = 60

x = 3

y = 20

xy = 60

x = 4

y = 15

xy = 60

The product of x and y is constant.

Finding the ratio between y to x :

x = 1

y = 60

y/x = 60

x = 2

y = 30

y/x = 15

x = 3

y = 20

y/x = 20/3

x = 4

y = 15

y/x = 15/4

The ratio between y to x is not constant. So, it is direct variation.

IDENTIFYING DIRECT ANG INVERSE VARIATION FROM TABLE

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling