IDENTIFY WHETHER THE NUMBER IS PRIME OR COMPOSITE

Tell whether the number is prime or composite.

Problem 1 :

7

Solution :

The number 7 is divisible only by 1 and the number itself.

So, 7 is a prime number.

Problem 2 :

16

Solution :

By decomposing 16, we get

The factors are 1, 2, 4, 8, 16.

The number 16 has more than two factors.

So, 16 is a composite number.  

Problem 3 :

21

Solution :

By decomposing 21, we get

The factors are 1, 3, 7, 21.

The number 21 has more than two factors.

So, 21 is a composite number. 

Problem 4 :

19

Solution :

The number 19 is divisible only by 1 and the number itself.

So, 19 is a prime number.

Problem 5 :

121

Solution :

By decomposing 121, we get

The factors are 1, 11, 121.

The number 121 has more than two factors.

So, 121 is a composite number.

Problem 6 :

51

Solution :

By decomposing 51, we get

The factors are 1, 3, 17, 51.

The number 51 has more than two factors.

So, 51 is a composite number.

Problem 7 :

84

Solution :

By decomposing 81, we get

The factors are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84.

The number 84 has more than two factors.

So, 84 is a composite number. 

Problem 8 :

141

Solution :

By decomposing 141, we get

141 does not end with 0, 2, 4, 6 or 8. So it is not divisible by 2.

Sum of the digits of 141 is 1 + 4 + 1 = 6 (divisible by 3). So, 141 is divisible by 3. Since it has more than 2 factors, it is composite numbers

The factors are 1, 3, 47, 141. 

Problem 9 :

The twin prime numbers out of the following are :

a)  2, 4    b) 3, 5    c)  7, 11    d) 13, 17

Solution :

Twin prime numbers are pairs of prime numbers that differ by 2. 

Option a :

• 2 is an even number and it is prime.
• 4 is even number, then it is composite.
• So, option a is not correct.

Option b :

• 3 is odd number and it is prime.
• 3 + 2 is 5, it is also prime number. So, these two are consecutive primes numbers.
• Option b is correct.

Problem 10 :

In the following which pair of numbers is co-primes ?

a)  (2, 4)   b)  (2, 3)    c) (3, 9)   d)  (4, 16)

Solution :

Option a :

2 and 4 are even numbers, then these are not co-primes.

Option b :

2 and 3 are odd numbers, then these are co-primes.

Option b is correct.

Problem 11 :

The sum of the prime numbers between 90 and 100 is

a)  188     b)  281   c)  376     d)  97

Solution :

Prime number between 90 and 100 is 97. So, option d is correct.

Problem 12 :

A prime number

a) has exactly one factor        b)  has exactly two factors 

c)  is not divisible by 2     d)  is an odd number

Solution :

A number which is divisble by 1 and itself is known as prime number. It has exactly two factors. So, option b is correct.

Problem 13 :

The least prime number is 

a)  1     b)  0     c)  2    d)  3

Solution :

2 is the even number and it is also prime. So, option c is correct.

Problem 14 :

A prime number is 

a) an even number     b)  an odd number    c) a composite number

d)  none

Solution :

• There is only one even prime number and it is 2.
• All odd numbers are not prime numbers. 
• A prime number cannot be a composite number.
• So, none option d is correct.

Problem 15 :

The smallest number of 4 digits exactly divisible by 12, 15, 20 and 35 is

a)  1000    b)  1160    c)  1260    d) none

Solution :

Least common multiple of 12, 15, 20 and 35

Least common multiple = 3 x 5 x 2 x 2 x 7

= 420

Multiples of 420 will be divisible by 12, 15, 20 and 35.

420, 840, 1260, ..........

So, option c is correct.

Problem 16 :

Successor of every even number is 

a)  even     b) prime    c)  odd    d)  none

Solution :

Let us consider an even number 20

20 + 1 = 21 (odd)

Successor of every even number is odd number.

Problem 17 :

Prime factors of 140 are 

a)  2 x 2 x 7      b)  2 x 2 x 5    c)  2 x 2 x 5 x 7     d)  2 x 2 x 5 x 7 x 3

Solution :

Decomposing 140 using prime factorization, we get

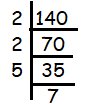
140 = 2 x 2 x 5 x 7

So, option c is correct.