HOW TO TELL IF A FUNCTION IS LINEAR FROM A TABLE

Identify if the table is linear or not. If it is, write the equation.

Problem 1 :

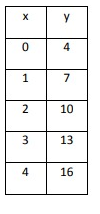
Solution:

In the above table, as x increases by 1, y increases by 3. The rate of change is constant. So, the above table represents a linear function.

Equation:

Let us choose (0, 4) and (1, 7).

Use the slope formula,

Slope-intercept form equation:

y = mx + b

Plug m = 3 and (x, y) = (0, 4)

4 = 3(0) + b

4 = 0 + b

b = 4

Now, plug m = 3 and b = 4 in slope-intercept form equation.

y = mx + b

y = 3x + 4

Problem 2 :

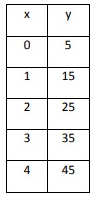
Solution:

In the above table, as x increases by 1, y increases by 10. The rate of change is constant. So, the above table represents a linear function.

Equation:

Let us choose (0, 5) and (1, 15).

Use the slope formula,

Slope-intercept form equation:

y = mx + b

Plug m = 10 and (x, y) = (0, 5)

5 = 10(0) + b

5 = 0 + b

b = 5

Now, plug m = 10 and b = 5 in slope-intercept form equation.

y = mx + b

y = 10x + 5

Problem 3 :

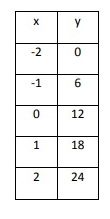
Solution:

In the above table, as x increases by 1, y increases by 6. The rate of change is constant. So, the above table represents a linear function.

Equation:

Let us choose (-2, 0) and (-1, 6).

Use the slope formula,

Slope-intercept form equation:

y = mx + b

Plug m = 6 and (x, y) = (-1, 6)

6 = 6(-1) + b

6 = -6 + b

b = 12

Now, plug m = 6 and b = 12 in slope-intercept form equation.

y = mx + b

y = 6x + 12

Problem 4 :

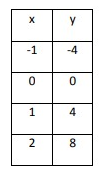
Solution:

In the above table, as x increases by 1, y increases by 4. The rate of change is constant. So, the above table represents a linear function.

Equation:

Let us choose (-1, -4) and (1, 4).

Use the slope formula,

Slope-intercept form equation:

y = mx + b

Plug m = 4 and (x, y) = (-1, -4)

-4 = 4(-1) + b

-4 = -4 + b

b = 0

Now, plug m = 4 and b = 0 in slope-intercept form equation.

y = mx + b

y = 4x + 0

y = 4x

Problem 5 :

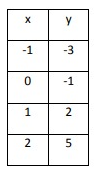
Solution:

In the above table, as x increases by 1, y increases by a greater amount each time. The rate of change is NOT constant. So, the above table represents a nonlinear function.

Problem 6 :

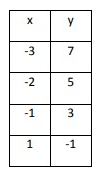
Solution:

In the above table, as x increases by 1,y decreases by 2. The rate of change is constant. So, the above table represents a linear function.

Equation:

Let us choose (-3, 7) and (-2, 5).

Use the slope formula,

Slope-intercept form equation:

y = mx + b

Plug m = -2 and (x, y) = (-3, 7)

7 = -2(-3) + b

7 = 6 + b

b = 1

Now, plug m = -2 and b = 1 in slope-intercept form equation.

y = mx + b

y = -2x + 1

Problem 7 :

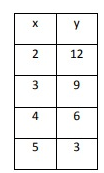
Solution:

In the above table, as x increases by 1, y decreases by 3. The rate of change is constant. So, the above table represents a linear function.

Equation:

Let us choose (2, 12) and (3, 9).

Use the slope formula,

Slope-intercept form equation:

y = mx + b

Plug m = -3 and (x, y) = (2, 12)

12 = -3(2) + b

12 = -6 + b

b = 18

Now, plug m = -3 and b = 18 in slope-intercept form equation.

y = mx + b

y = -3x + 18

Problem 8 :

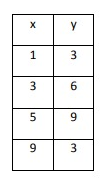
Solution:

In the above table, as x increases by 2, y increases by a greater amount each time. The rate of change is NOT constant. So, the above table represents a nonlinear function.