HOW TO PLOT INEQUALITIES ON A NUMBER LINE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
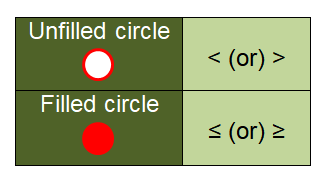
To plot the given inequalities in the number line, we must know the below rules.
1. If we have the inequality
< (less than) or > (greater than),
we have to use the empty / unfilled circle.
2. If we have the inequality sign
≤ (less than or equal to) or ≥ (greater than or equal to),
we have to use the filled circle.
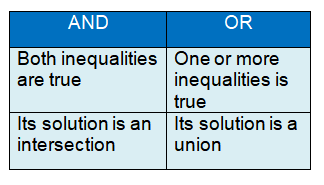
Also we must know the meaning of two words "And & Or".
Draw a number line graph of:
Problem 1 :
{x│-2 ≤ x ≤ 3}
Solution :
-2 ≤ x ≤ 3
Since the given inequalities -2 ≤ x ≤ 3 (less than or equal and less than or equal), we draw the line from -2 with a filled circle to 3 with a filled circle on the number line.
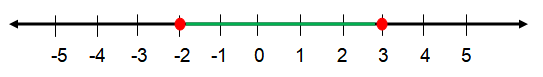
Problem 2 :
{x│0 < x < 3}
Solution :
Since the given inequalities 0 < x < 3 (less than and less than), we draw the line from 0 with an unfilled circle to 3 with an unfilled circle on the number line.

Problem 3 :
{x │ x < 1 or x > 3}
Solution :
Given, x < 1 or x > 3 is a compound inequality OR.
Since the first inequality x < 1 (less than), so we draw the line left side from 1 with an unfilled circle on the number line.
Since the second inequality x > 3(greater than), so we draw the line right side from 3 with an unfilled circle on the number line.

Problem 4 :
{x│ x ≤ 2 or x ≥ 3}
Solution :
Given, x ≤ 2 or x ≥ 3 is a compound inequality OR.
Since the first inequality x ≤ 2 (less than or equal), so we draw the line left side from 2 with a filled circle on the number line.
Since the second inequality x ≥ 3(greater than or equal), so we draw the line right side from 3 with a filled circle on the number line.
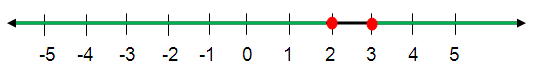
Problem 5 :
{x│ x ≤ -2 or x > 1}
Solution :
Given, x ≤ -2 or x > 1 is a compound inequality OR.
Since the first inequality x ≤ -2 (less than or equal), so we draw the line left side from 2 with a filled circle on the number line.
Since the second inequality x > 1(greater than), so we draw the line right side from 1 with an unfilled circle on the number line.

Problem 6 :
{x│-1 < x ≤ 4}
Solution :
Since the given inequalities -1 < x ≤ 4 (less than and less than or equal), we draw the line from -1 with an unfilled circle to 4 with a filled circle on the number line.

Problem 7 :
{x│ -3 ≤ x < 0}
Solution :

Problem 8 :
{x│ x < 0 or x ≥ 4}
Solution :

Problem 9 :
{x│ x ≤ -1 or 0 ≤ x ≤ 3}
Solution :

Problem 10 :
{x│ -2 ≤ x ≤ 2 or x ≥ 4}
Solution :
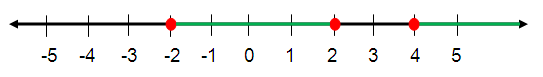
Problem 11 :
Write the sentence as an inequality.
a) A number x is greater than 3.
b) A number n plus 7 is less than or equal to 9.
c) Fifteen is no more than a number t divided by 5.
d) Three times a number w is less than 18
e) One-half of a number y is more than 22.
f) Three is less than the sum of a number s and 4.
g) Thirteen is at least the difference of a number v and 1.
h) Four is no less than the quotient of a number x and 2.1
Solution :
a) A number x is greater than 3.
x > 3
b) A number n plus 7 is less than or equal to 9.
n + 7 ≤ 9
c) Fifteen is no more than a number t divided by 5.
15 ≤ t/5
d) Three times a number w is less than 18
3w < 18
e) One-half of a number y is more than 22.
1/2 of y < 22
y/2 < 22
f) Three is less than the sum of a number s and 4.
3 < s + 4
g) Thirteen is at least the difference of a number v and 1.
13 > v - 1
h) Four is no less than the quotient of a number x and 2.1
4 < x/2.1
Problem 12 :
The winner of a weight-lifting competition bench-pressed 400 pounds. The other competitors all bench-pressed at least 23 pounds less.
a. Write an inequality that represents the weights that the other competitors bench-pressed.
b. Was one of the other competitors able to bench-press 379 pounds? Explain.
Solution :
Weight lifted by winner = 400 pounds
The other competitor pressed at least 23 pounds less
a) The competitor bench presses that weights 400 - 23 ==> 377 pounds
If w represents the weight in pounds lifted by another competitor, the condition is represented by the inequality:
w ≤ 377
b) No, one of the other competitors was not able to bench-press 379 pounds.
According to the inequality w≤377w is less than or equal to 377𝑤≤377 derived from the problem's conditions, all other competitors lifted a weight less than or equal to 377 pounds. Since 379>377. 379 is greater than 377379>377, this weight is outside the range of possible weights for the other competitors.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling