HOW TO FIND THREE DIFFERENT REPRESENTATIONS OF A POLAR POINT

Find all pairs of polar coordinates that describe the same point as the provided polar coordinates.

Problem 1 :

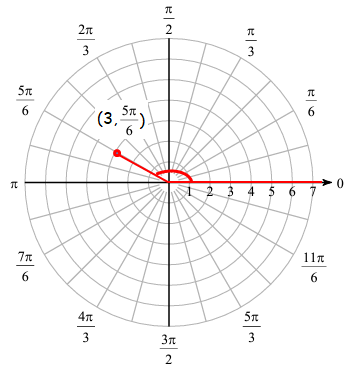
(3, 5π/6)

Solution :

Here r = 3 and θ = 5π/6. 

Here radius is positive and angle is positive. So we can go counter clockwise direction to get 5π/6.

First point :

Second point :

By finding coterminal angle, we can get more points or we  use the formula (r, θ + 2kπ). Here we apply k = -1.

= (3, ((5π/6) - 2π))

= (3, (5π - 12π/6))

= (3, (- 7π/6))

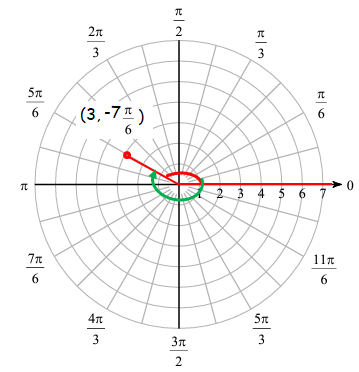
Third point :

Now we may do reflection to get the other point. If we use formula (-r, θ + (2k+1) π), then we apply k = 0 and change radius as negative.

= (-3, (5π/6)+ π)

= (-3, (5π + 6π)/6))

= (-3, (11π/6))

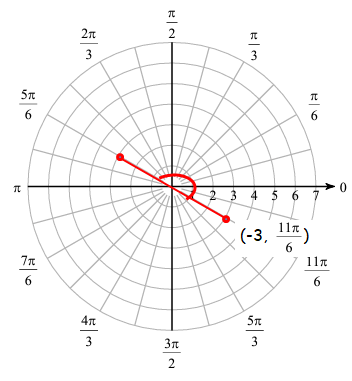
Fourth point :

Finding coterminal angle of 11π/6, we get

= (11π/6) - 2π

= (11π - 12π)/6

= -π/6

So, the three different representation of polar point (3, 5π/6) are 

 (3, (- 7π/6)), (-3, (11π/6)) and (-3, -π/6)

Note :

We can get infinitely many points.

Problem 2 :

(-4, π/12)

Solution :

Here r = -4 and θ = π/12. 

First point :

(-4, π/12)

Second point :

Finding reference angle,

(-4, (π/12) - 2π))

(-4, -23π/12)

Third point :

Since the radius is negative, we can do the reflection

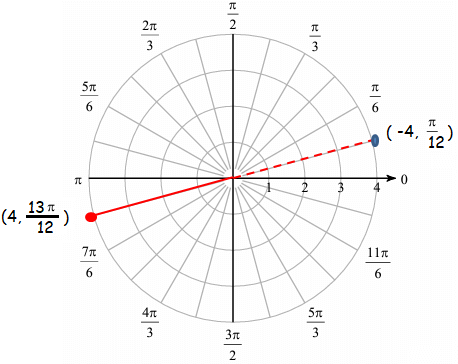
(4, 13π/12)

Fourth point :

By finding reference angle 

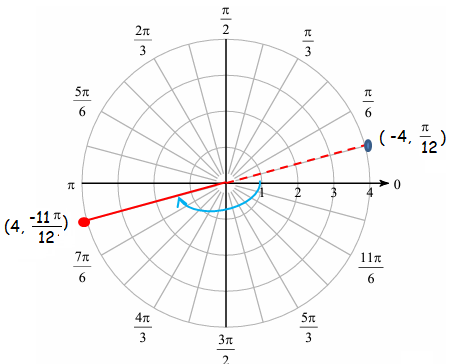
(4, -11π/12)

Other way using formula :

(r, θ + 2kπ) or (-r, θ + (2k+1) π)

Considering the given point as (r, θ) which is (-4, π/12)

(r, θ + 2kπ)

• When k = 0, then (4, π/12)
• When k = -1, then (4, (π/12) - 2π)) ==> (4, (-23π/12))

Changing sign of r, then the new point will be in the form

(-r, θ + (2k+1) π)

• When k = 0, then (-4, π/12 + π) ==> (-4, 13π/12)
• When k = -1, then (4, (π/12) - π)) ==> (4, (-11π/12))

So, the three different representation of the point (-4, π/12) are

(4, (-23π/12)), (-4, 13π/12) and (-4, (-11π/12))

Problem 3 :

(2, -3π/2)

Solution :

Here r = 2 and θ = -3π/2. 

Given point :

(2, -3π/2)

Let us find the alternate point using formula,

(r, θ + 2kπ)

When k = 1

First point :

= (2, -3π/2 + 2π)

= (2, π/2)

Using the formula (-r, θ + (2k+1) π), we may find the other two points.

Second point : 

When k = 0

= (-2, -3π/2 + π)

= (-2, π/2)

Third point : 

When k = 1

= (-2, -3π/2 + 3π)

= (-2, 3π/2)

So, the three different representation of the point (2, -3π/2) are 

(2, π/2), (-2, π/2), (-2, 3π/2)

Problem 4 :

(-4, -7π/6)

Solution :

Here r = -4 and θ = -7π/6 

Given point :

(-4, -7π/6)

Let us find the alternate point using formula,

(r, θ + 2kπ)

When k = 1

First point :

= (-4, -7π/6 + 2π)

= (-4, 5π/2)

Using the formula (-r, θ + (2k+1) π), we may find the other two points.

Second point : 

When k = 0

= (4, -7π/6 + π)

= (4, -π/6)

Third point : 

When k = 1

= (4, -7π/6 + 3π)

= (4, 11π/6)

So, the three different representation of the point (-4, -7π/6)are 

(-4, 5π/2), (4, -π/6) and (4, 11π/6)

Problem 5 :

(2, 23π/12)

Solution :

Here r = 2 and θ = 23π/12

Given point :

(2, 23π/12)

Let us find the alternate point using formula,

(r, θ + 2kπ)

When k = -1

First point :

= (2, 23π/12 - 2π)

= (2, -π/12)

Using the formula (-r, θ + (2k+1) π), we may find the other two points.

Second point : 

When k = -1

= (-2, 23π/12 - π)

= (-2, 11π/12)

Third point : 

When k = -2

= (-2, 23π/12 - 3π)

= (-2, -13π/12)

So, the three different representation of the point (2, 23π/12) are 

(2, -π/12), (-2, 11π/12) and (-2, -13π/12)