HOW TO FIND THE VALUE OF UNKNOWN IN SIMILAR FIGURES

The two polygons are similar. Find the value of x.

Problem 1 :

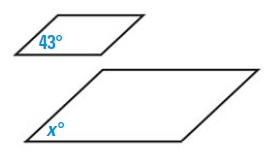
Solution :

The two polygons are similar.

x = 43

Problem 2 :

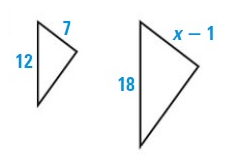
Solution :

The two polygons are similar.

12/18 = 7/(x - 1)

Using cross multiplication.

12(x – 1)  = 18(7)

12x - 12 = 126

12x = 126 + 12

12x = 138

x = 11.5

Problem 3 :

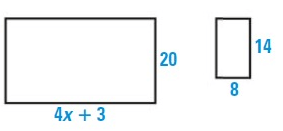
Solution :

The two polygons are similar.

(4x + 3)/8 = 20/14

Using cross multiplication.

14(4x + 3) = 20(8)

56x + 42 = 160

Subtracting 42

56x = 160 - 42

56x = 118

x = 118/52

x = 2.27

Problem 4 :

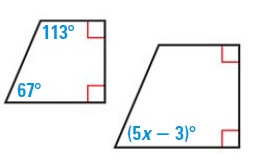
Solution :

The two polygons are similar.

67^º = (5x – 3)^º

67 + 3 = 5x

70 = 5x

x = 14

Problem 5 :

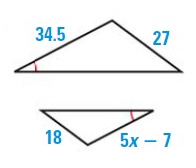
Solution :

The two polygons are similar.

27/18 = 34.5/(5x - 7)

27(5x - 7) = 34.5(18)

135x - 189 = 621

135x = 621 + 189

135x = 810

x = 810/135

x = 6

Problem 6 :

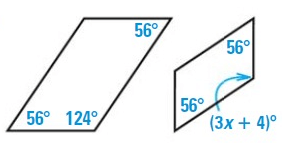
Solution :

The two polygons are similar.

124^º = (3x + 4)^º

124 – 4 = 3x

120 = 3x

x = 120/3

x = 40

Problem 7 :

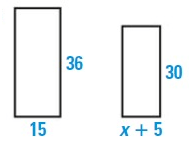
Solution :

The two polygons are similar.

36/30 = 15/(x + 5)

Using cross multiplication.

36(x + 5) = 30 × 15

36x + 180 = 450

Subtracting 180 on both sides.

36x = 450 – 180

36x = 270

x = 7.5

Problem 8 :

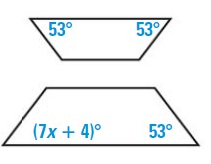
Solution :

The two polygons are similar.

(7x + 4)^º = 53^º

7x = 53 – 4

7x = 49^º

x = 49/7

x = 7

Problem 9 :

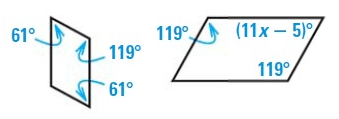
Solution :

The two polygons are similar.

61^º= (11x – 5)^º

61 + 5 = 11x

66 = 11x

66/11 = x

x = 6

Problem 10 :

Figure A has a perimeter of 60 inches and one of the side lengths is 5 inches. Figure B has a perimeter of 84 inches. Find the missing corresponding side length.

Solution :

Let x be the missing side.

Side length of figure A : side length of figure B = Perimeter of figure A : perimeter of figure B

5 : x = 60 : 84

5/x = 60/84

60x = 5(84)

x = 5(84) / 60

x = 7

So, the missing side is 7 inch.

Problem 11 :

Figure A has an area of 4928 square feet and one of the side lengths is 88 feet. Figure B has an area of 77 square feet. Find the missing corresponding side length.

Solution :

Let x be the missing side.

(Side length of figure A : side length of figure B)² = Area of figure A : Area of  figure B

88² : x²  = 4928 : 77

7744 : x²  = 4928 : 77

7744 / x² = 4928 / 77

4928x² = 7744(77)

x² = 7744(77)/4928

x² = 7744(77)/4928

x² = 379456

x = √379456

x = 616

So, the measure of missing side is 616 feet.

Problem 12 :

In the diagram triangle ABC ~ triangle ADE

a) Find the scale factor from triangle ABC to ADE

b) Find the value of x

c) Find <ABC

d) The perimeter of triangle ABC is about 42.4 units. Find the perimeter of triangle ADE.

e) The area of triangle ABC is about 71.75 square units. Find the area of triangle ADE

f) Is BC || DE explain your reasoning.

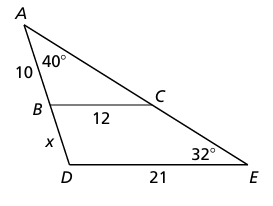
Solution :

In the diagram triangle ABC ~ triangle ADE

a) Comparing the corresponding sides, 

AB : AD = AC : AE = BC : DE

The scale factor is 12 : 21

= 12/21

= 4 / 7

= 4 : 7

b)

10 : (10 + x) = 12 : 21

10/(10 + x) = 12/21

21(10) = 12(10 + x)

210 = 120 + 12x

210 - 120 = 12x

90 = 12x

x = 90/12

x = 7.5

c) ∠ABC = ∠ADE

∠ADE = 180 - (40 + 32)

= 180 - 72

∠ADE = 108

∠ABC = 108

d) Perimeter of triangle ABC : Perimeter of triangle ADE = 12 : 21

42.4 : Perimeter of triangle ADE = 12 : 21

42.4/Perimeter of triangle ADE = 12/21

Perimeter of triangle ADE (12) = 42.4(21)

Perimeter of triangle ADE = 42.4(21) / 12

= 74.2

e) The area of triangle ABC = 71.75 square units.

Area of triangle ABC : Area of triangle ADE = 12² : 21²

71.75/Area of triangle ADE = 144 / 441

71.75(441) = 144 (Area of triangle ADE)

Area of triangle ADE = 71.75(441) / 144

= 219.73 square units.

f) Since corresponding sides are equal, the sides BC and DE are parallel.

Problem 13 :

ABCDE ~ KLMNP 

a) Find the scale factor from ABCDE to KLMNP.

b) Find the scale factor from KLMNP to ABCDE.

c) Find the values of x, y, and z.

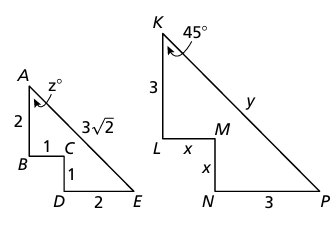
d) Find the perimeter of each polygon.

e) Find the ratio of the perimeters of ABCDE to KLMNP.

f) Find the ratio of the areas of ABCDE to KLMNP.

Solution :

a) The scale factor from ABCDE to KLMNP = 2 : 3

b) The scale factor from KLMNP to ABCDE = 3 : 2

c) 

d) Perimeter of polygon ABCDE = 2 + 1 + 1 + 2 + 3√2

= 6 + 3√2

Perimeter of polygon KLMNP = 3 + x + x + 3 + y

= 3 + 3/2 + 3/2 + 3 + 4.5√2

= 9 + 4.5√2

e) Since the corresponding sides is in the ratio 2 : 3, then the perimeter will also be in the same ratio.

f)

Area of ABCDE = Area of triangle - area of square

= (1/2) ⋅ 3 ⋅ 3 - 1 ⋅ 1

= 9/2 - 1

= 4.5 - 1

= 3.5 square units

Area of KLMNP = (1/2) ⋅ 4.5 ⋅ 4 - 3/2 ⋅ 3/2

= 9 - 9/4

= 9 - 2.25

= 6.75 square units