HOW TO FIND THE IMAGE EQUATION OF THE LINE

Problem 1 :

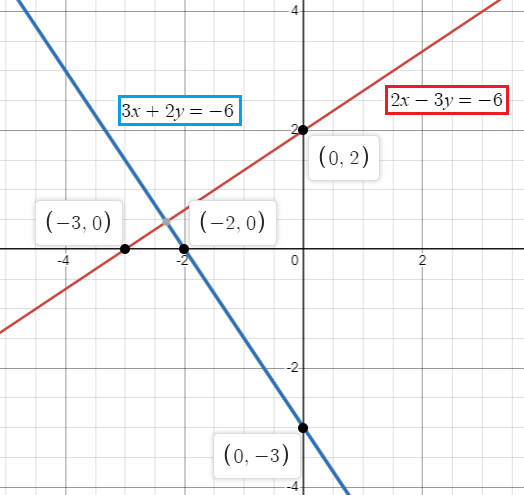
Find the image equation of the line 2x - 3y = -6 under a clockwise rotation about O (0, 0) through 90°.

Solution :

Equation of the given line :

2x - 3y = -6

When a point is rotated with clockwise rotation about 90°

(x, y) --> (y, -x)

By replacing x = y and y = -x, we get

2y - 3(-x) = -6

2y + 3x = -6

3x + 2y = -6

Problem 2 :

Find the image equation when 

y = 2x is rotated clockwise through 90° about O(0, 0)

Solution :

Since we use 90° clockwise rotation, we have to follow the rule

(x, y) --> (y, -x)

y = 2x

Applying x = y and y = -x

-x = 2y

x = -2y

Problem 3 :

Find the image equation when 

y = -3 is rotated counter clockwise through 90° about O(0, 0)

Solution :

Since we use 90° counter clockwise rotation, we have to follow the rule

(x, y) --> (-y, x)

y = -3

Applying x = -y and y = x

x = -3

Problem 4 :

Find the image equation of the line 3x + 2y = 3 under an anticlockwise rotation 90° about O(0, 0)

Solution :

Since we use 90° counter clockwise rotation, we have to follow the rule

(x, y) --> (-y, x)

3x + 2y = 3

Applying x = -y and y = x

3(-y) + 2x = 3

-3y + 2x = 3

2x - 3y = 3

Problem 5 :

Find the equation of the image line when 

y = 2x + 3 is translated (-1, 2)

Solution :

Translation with (h, k)

x' = x - h and y' = y - k

x' = x - (-1) ==> x' = x + 1

y' = y - 2

Given equation, y = 2x + 3

After applying these changes, we get

y - 2 = 2(x + 1) + 3

y - 2 = 2x + 2 + 3

y - 2 = 2x + 5

y = 2x + 5 + 2

y = 2x + 7

Problem 6 :

Find the equation of the image line when 

y = (1/3) x + 2 is translated (3, 0)

Solution :

Translation with (h, k)

x' = x - 3 and y' = y - 0

Given equation, y = (1/3) x + 2

After applying these changes, we get

y - 0 = (1/3)(x - 3) + 2

y = (1/3)x - (1/3)⋅3 + 2

y = (1/3)x - 1 + 2

y = (1/3)x + 1

Problem 7 :

Find the equation of the image line when 

y = -x + 2 is translated (2, 3)

Solution :

Translation with (h, k)

x' = x - 2 and y' = y - 3

Given equation, y = -x + 2

y - 3 = -(x - 2) + 2

y - 3 = -x + 2 + 2

y - 3 = -x + 4

x + y = 4 + 3

x + y = 7

Problem 8 :

Find the equation of the image line when 

y = -(1/2)x is translated (-2, -5)

Solution :

Translation with (h, k)

x' = x - (-2) and y' = y - (-5)

x' = x + 2 and y' = y + 5

Given equation, y = -(1/2)x

y + 5 = -(1/2)(x + 2)

y + 5 = -(1/2)x + (-1/2)⋅2

y + 5 = -(1/2)x - 1

y = -(1/2)x - 1 - 5

y = -(1/2)x - 6

Problem 8 :

Find the image of (2, 3) under clockwise 90 degree rotation about (0, 0) followed by a reflection in the x-axis.

Solution :

Rotation clockwise about 90 degree :

(Ix, y) --> (y, - x)

(2, -3) --> (-3, -2)

Reflection about x-axis :

put y = -y

(-3, -2) --> (-3, 2)

Problem 9 :

Find the equation of the image when y = 2x 

i) enlarged with center (0, 0) and a scale factor k = 3

ii)  reduced with center (0, 0) and a scale factor k = 1/3

Solution :

i) Enlarging with the factor of k = 3

(x, y) -> (3x, 3y)

y = 2x

After applying these changes,

3y = 2(3x)

3y = 6x

y = 2x

ii)  Reducing with the factor of k = 1/3

(x, y) -> (x/3, y/3)

y = 2x

After applying these changes,

y/3 = 2(x/3)

y = 2x