HOW TO FIND DIAGONALS OF A KITE GIVEN THE AREA

To find diagonal, we have the following ways.

(i) From the given area and one diagonal, find the other diagonal.

(ii) Using Pythagorean theorem, find length of diagonal.

The diagonals of a kite are perpendicular to each other. The longer diagonal of the kite bisects the shorter diagonal.

Area of kite ?

A kite is a quadrilateral which has two pairs of adjacent sides equal in length.

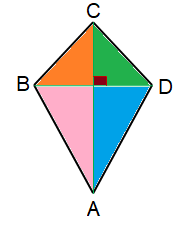
To find area of kite we need diagonals.

Area of kite = (1/2) x diagonal 1 x diagonal 2

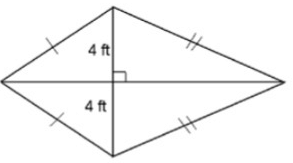
Problem 1 :

The area of this shape is 48 ft². Solve for x. 

Solution :

By observing the figure, length of one diagonal is given.

Area of a kite = 1/2 d₁d₂

Let x be the another diagonal.

48 = 1/2 (8)(x)

48 = 4x

Divide both sides by 4.

48/4 = 4x/4

12 = x

So, the value of x is 12

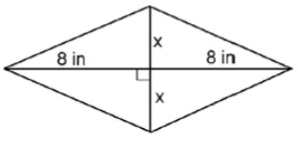
Problem 2 :

The area of this shape is 32 in². Solve for x. 

Solution :

This is a rhombus.

Area of a rhombus = 1/2 d₁d₂

d₁ = 8 + 8 = 16

d₂ = x + x = 2x

32 = 1/2 (16)(2x)

32 = 8(2x)

x = 32/16

x = 2

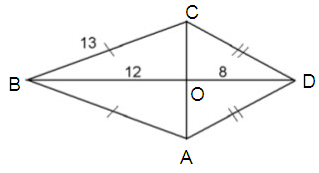
Problem 3 :

Find the area of the kite given below,

Solution :

In kite, the diagonal will bisect each other at right angles.

To figure out OC,

Use Pythagorean Theorem :

(BC)² = (CO)² + (BO)²

(13)² = (CO)² + (12)²

169 = (CO)² + 144

Subtract 144 from both sides.

25 = (CO)²

CO = 5, then CA = 2(5) ==> 10

Area of a kite = 1/2 d₁d₂

 = 1/2 (10)(20)

 = 1/2 (200)

= 100

So, area of a kite is 100.

Find the length of missing diagonal in each kite.

Problem 4 :

Find TR if QS = 24 ft 

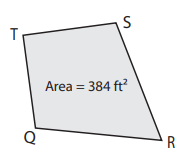
Solution :

Area of kite = (1/2) x TR x SQ

Here area = 384 and SQ = 24 ft

Applying these values, we get

384 = (1/2) x TR x 24

TR = 384/12

TR = 32

Problem 5 :

Find VX if WU = 28 in.

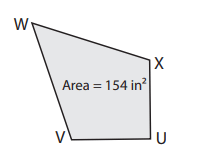
Solution :

Area of kite = (1/2) x WU x VX

Here area = 154 and WU = 28 in

Applying these values, we get

154 = (1/2) x 28 x VX

154 = 14 VX

VX = 154/14

VX = 11 in