HOW TO FIND THE DERIVATIVE OF A INVERSE FUNCTION

Problem 1 :

Let f(x) = x² - (3/x)

a) What is the value of f^-1(8) ?

b) What is the value of (f^-1)' (8) ?

Solution :

In a function y and f(x) both are equal. That is,

y = f(x)

f^-1(y) = x

a)  Given that,

f(x) = x² - (3/x)

In f^-1(8), y = 8. Then f(x) = 8

8 = (x³ - 3)/x

8x = x³ - 3

x³ - 8x - 3 = 0

Solving using synthetic division, we get

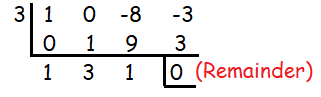
3 is a solution. So, the value of f^-1(8) is 3.

b) 

Problem 2 :

If f(2) = 5 and f'(2) = 1/4, find (f^-1)' (5)

Solution :

(f^-1)' (x) = 1/f' [(f^-1) (x)]

Given that, f(2) = 5

f^-1(5) = 2

Given that, f'(2) = 1/4

(f^-1)' (1/4) = 2

(f^-1)' (5) = 1/f' [(f^-1) (5)]

Applying the value of (f^-1) (5) = 2 in above, we get

= 1/f' (2)

Applying the value of f' (2) = 4 in above,

= 1/(1/4)

= 1 (4/1)

= 4

So, the answer is 4.

Problem 3 :

Let f and g be functions that are differentiable everywhere. If g is the inverse function of f and if g(3) = 4 and f'(4) = 3/2, then g'(3) ?

a)  1/4    b)  1/3    c)  2/3    d)  4/3

Solution :

Given that g(3) = 4,

Since g and f are inverse to each other.

f(g(x)) x

f'(g(x)) g'(x) = 1

f'(g(3)) g'(3) = 1

Applying the value of g(3), we get

f'(4) g'(3) = 1

g'(3) = 1/f'(4)

Applying the value of f'(4), we get

g'(3) = 1/(3/2)

= 1 x (2/3)

g'(3) = 2/3

So, the answer is option c.

Problem 4 :

If f(-3) = 2 and f'(-3) = 3/4, then (f^-1)' (2) = ?

a)  1/2   b)  4/3     c)  3/2     d)  -3/4

Solution :

Given that f(-3) = 2

f^-1(2) = -3

(f^-1)' (x) = 1/f' [(f^-1) (x)]

(f^-1)' (2) = 1//f' [(f^-1) (2)]

Applying the value of (f^-1) (2) = -3, we get

= 1/f' (-3)

Applying the value of f' (-3) = 3/4, we get

= 1/(3/4)

= 4/3

So, the answer is 4/3.

Problem 5 :

If f(x) = x³ - x + 2, then (f^-1)^'(2) = ?

Solution :

f(x) = x³ - x + 2

f'(x) = 3x² - 1 + 0

 f'(x) = 3x² - 1

(f^-1)^'(2) = 1/f'( (f^-1)(2) ) ----(1)

Finding the value of  (f^-1)(2) :

2 = x³ - x + 2

0 = x³ - x

x(x² - 1) = 0

x = 0, x = 1 and -1.

So, the value of (f^-1)(2) are 0, 1 and -1.

Applying these values one by one, we get

(f^-1)^'(2) = 1/f' (0 )

Evaluating f'(0) from f'(x) = 3x² - 1 :

 f'(0) = 3(0)² - 1 ==> -1

Applying this value in (1), we get

= 1/(-1)

= -1

Evaluating f'(1) from f'(x) = 3x² - 1 :

 f'(1) = 3(1)² - 1 ==> 2

Applying this value in (1), we get

= 1/2

Evaluating f'(-1) from f'(x) = 3x² - 1 :

 f'(-1) = 3(-1)² - 1 ==> 2

Applying this value in (1), we get

= 1/2

Problem 6 :

If f(x) = sin x, then (f^-1)' (√3/2) = ?

a)  1/2   b)  2√3/3    c)  √3    d)  2

Solution :

(f^-1)' (√3/2) = 1/f'( (f^-1) (√3/2) ) ---(1)

f(x) = sin x

Finding (f^-1) (√3/2) :

√3/2 = sin x

x = sin^-1(√3/2)

x = π/3

 (f^-1) (√3/2)  = π/3

Applying this value in (1), we get

(f^-1)' (√3/2) = 1/f'(π/3)

from f(x) = sin x, f'(x) = cos x

f'(π/3) = cos (π/3)

(f^-1)' (√3/2) = 1/2

So, the answer is 1/2.

Problem 7 :

If f(x) = 1+ ln x, then (f^-1)' (2)

a)  -1/e    b)  1/e    c)  -e    d) e

Solution :

If (x) = 1+ ln x

(f^-1)' (2) = 1/f'((f^-1) (2))  ----(1)

Finding (f^-1) (2)) :

f (x) = 1 + ln x

2 = 1 + ln x

1 = ln x

x = e¹

x = e

 (f^-1) (2)) = e

The value of  (f^-1) (2)) is e.

(f^-1)' (2) = 1/f'(e)

From f(x) = 1 + ln x

f'(x) = 0 + 1/x

f'(x) = 1/x

f'(e) = 1/e

Then, (f^-1)' (2) = 1/f'(e)

(f^-1)' (2) = 1/(1/e)

= e

So, the answer is e.