HOW TO FIND THE AREA OF A QUADRILATERAL

Find the area of each Parallelogram .

Problem 1 :

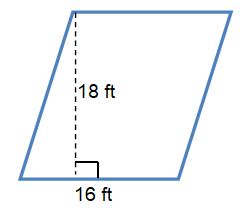
Solution :

By observing the figure, 

Base (b) = 16 ft and Height (h) = 18 ft

Area of a Parallelogram A = b × h sq. units.

= 16 ×18

Area = 288 ft²

Problem 2 :

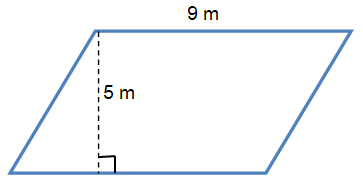
Solution :

By observing the figure, 

Base (b) = 9 m and Height (h) = 5 m

Area of a Parallelogram  A = b × h sq. units.

= 8 × 9

Area = 72 m²

Find the area of each trapezoid .

Problem 3 :

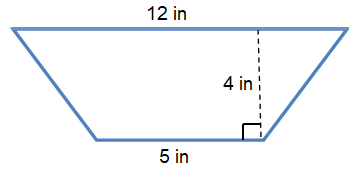
Solution :

By observing the figure,

Base (b₁) = 12 in, Base (b₂) = 5 in and Height (h) = 4 in.

Area of a trapezoid A = 1/2 (b₁ + b₂) × h

= 1/2 (12 in + 5 in) × 4 in

= 1/2 (17 in) × 4 in

Area = 34 in²

Problem 4 :

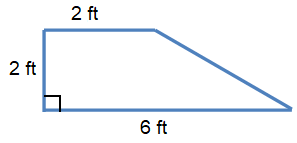
Solution :

By observing the figure,

Base (b₁) = 6 ft, Base (b₂) = 2 ft, and Height (h) = 2 ft

Area of a trapezoid A = 1/2 (b₁ + b₂) × h

= 1/2 (6 + 2) × 2

= 1/2 (8) × 2

Area = 8 ft²

Find the area of each rhombus.

Problem 5 :

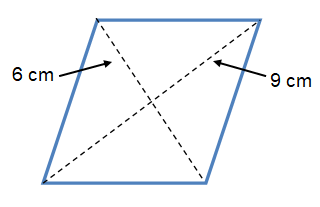
Solution :

By observing the figure,

Diagonal (d₁) = 6 cm and Diagonal (d₂) = 9 cm

Area of a rhombus A = 1/2 (d₁ × d₂) 

= 1/2 (6 × 9)

= 1/2 (54)

= 27 cm²

Problem 6 :

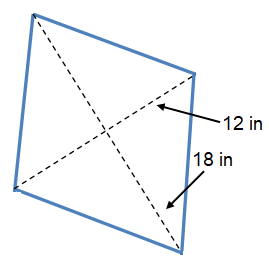
Solution :

By observing the figure,

Diagonal (d₁) = 12 in. and Diagonal (d₂) = 18 in.

Area of a rhombus A = 1/2 (d₁ × d₂) 

= 1/2 (12 in × 18 in)

= 1/2 (216 in²)

Area = 108 in²

Problem 7 :

A desktop in the shape of a parallelogram has a base of 30 inches and a height of 40 inches. What is the area of the desktop?

Solution :

Given,

Base of the desktop (b) = 30 in

Height of the desktop (h) = 40 in

To find the area of the desktop,

Area of a Parallelogram A = b × h

= 30 × 40

= 1200 in²

So, the area of the desktop = 1200 in²

Problem 8 :

A rhombus has one diagonal that is 14 centimetres long and one diagonal that is 12 centimetres long. What is the area of the rhombus?

Solution :

Given,

Diagonal (d₁) = 14 cm and Diagonal (d₂) = 12 cm

Area of a rhombus A = 1/2 (d₁ × d₂) 

= 1/2 (14 × 12)

= 1/2 (168)

= 84 cm²

So, the area of the rhombus = 84 cm².

Problem 9 :

The bases of a trapezoid are 24 feet and 16 feet. The height of the trapezoid is12 feet. What is the area of the trapezoid?

Solution :

Given,

Base (b₁) = 24 ft, Base (b₂) = 16 ft and Height (h) = 12 ft

Area of a trapezoid A = 1/2  (b₁ + b₂) × h

= 1/2  (24 + 16) × 12

= 1/2 (40) × 12

= 240 ft²

So, the area of the trapezoid = 240 ft²

Problem 10 :

The area of a rhombus is 150 cm². The lenght of one of its diagonals is 10 cm. The length of other diagonal is :

Solution :

Area of rhombus = (1/2) x d₁ x d₂

(1/2) x d₁ x d₂ = 150

Length of one diagonal = 10 cm, length of other diagonal = ?

(1/2) x 10 x d₂ = 150

d₂ = 150/5

d₂ = 30

So, the length of the other diagonal is 30 cm.

Problem 11 :

The total area of the polygon is 176 square feet. Find the value of x.

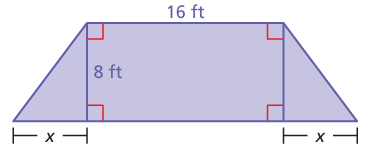
Solution :

Area of polygon = 2(area of triangle) + area of rectangle

Area of triangle = (1/2) x base x height

= (1/2) ⋅ x ⋅ 8

= 4x

Area of rectangle = length ⋅ width

= 16 ⋅ 8

= 128

2(Area of triangle) = 2(4x) ==> 8x

8x + 128 = 176

8x = 176 - 128

8x = 48

x = 48/8

x = 6

So, the base of the triangle is 6 ft.

Problem 12 :

The rectangle and the trapezoid have the same area. What is the length ℓ of the rectangle?

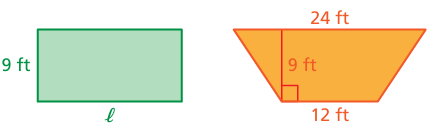
Solution :

Area of rectangle = Area of quadrilateral

length ⋅ width = (1/2) ⋅ height ⋅ sum of length of parallel sides

9 ⋅ l = (1/2) ⋅ 9 ⋅ (12 + 24)

9 ⋅ l = (1/2) ⋅ 9 ⋅ 36

9 ⋅ l =  9 ⋅ 18

l = (9 ⋅ 18)/9

l = 18

So, the length of the rectangle is 18 ft.

Problem 13 :

The triangle and the trapezoid share a 15-inch base and a height of 10 inches.

a. The area of the trapezoid is less than twice the area of the triangle. Find the values of x. Explain your reasoning.

b. Can the area of the trapezoid be exactly twice the area of the triangle? Explain your reasoning.

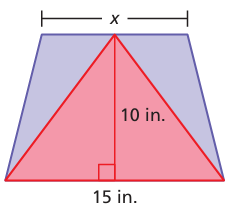
Area of trapezoid = (1/2) x 10 x (15 + x)

= 5(15 + x)

Area of triangle = (1/2) x 15 x 10

= 5 (15)

= 75 square inches

a)  Area of trapezoid < area of triangle

5(15 + x) < 150

15 + x < 150/5

15 + x < 30

x < 30 - 15

x < 15

The possible values of x are lesser than 15.

b)  When x = 15, the area of the trapezoid will be twice the area of triangle.