HOW TO FIND SURFACE AREA OF SIMILAR SOLIDS

If two figures are similar then:

• the figures are equiangular, and
• the corresponding sides are in proportion.

Surface area of similar figures :

If two solids are similar, then the ratio of their surface areas is equal to the square of the ratio of their corresponding linear measures. 

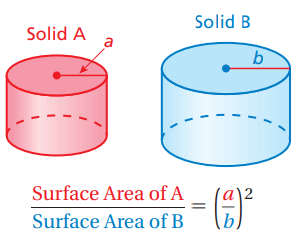
The solids are similar. Find the surface area S of the red solid. Round your answer to the nearest tenth.

Problem 1 :

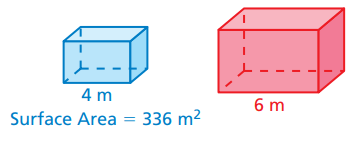
Solution :

Surface area of small solid = k² x surface area of large solid

Surface area of small solid = 336 m²

Scale factor = (4/6) ==> 2/3

336 = (2/3)² x surface area of large solid

surface area of large solid = 336 (9/4)

= 756 m²

Problem 2 :

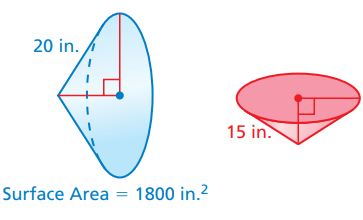
Solution :

Surface area of large solid = k² x surface area of small solid

Surface area of large solid = 1800 in²

Scale factor = (20/15) ==> 4/3

1800 = (4/3)² x surface area of small solid

surface area of small solid = 1800 (9/16)

= 1012.5 in²

Problem 3 :

The ratio of the corresponding linear measures of two similar cans of fruit is 4 to 7. The smaller can has a surface area of 220 square centimeters. Find the surface area of the larger can

Solution :

Surface area of smaller can = 220

Ratio between small can to large can = 4 : 7

Surface area of small can = (4/7)² x Surface area of large can

220 = (16/49) x Surface area of large can

Surface area of large can = 220(49/16)

= 673.75 square centimeters

Problem 4 :

A model of sky scraper was made with the scale factor of  3 : 13. What is the ratio of the surface area of model to the surface area of original sky scrapers?

Solution :

Ratio between model to original sky scraper = 3 : 13

Ratio between surface area of model to original sky scraper

= 3² : 13²

= 9 : 169

Problem 5 :

Each pair of figures is similar. Find the scale factor of the figure on the left to the figure on the right. Then find

(i)  the ratio of surface areas

and

(ii)  the ratio of volumes.

Solution :

Slant height of the large cone : Slant height of the small cone

200 = 160

5 : 4

So, the two cone are in the ratio is 5 : 4.

(i)  The surface area of the two cones will be in the ratio :

5² : 4²

So, the ratio of surface area is 25 :16

(ii)  The volume of these two cones will be in the ratio :

5³ : 4³

So, the ratio of volume is 125 : 64.

Problem 6 :

Solution :

Height of the large prism : height of the small prism

42 : 24

7 : 4

So, the two prism are in the ratio is 7: 4.

(i)  The surface area of the two prism will be in the ratio :

7² : 4²

So, the ratio of surface area is 49:16

(ii0  The volume of these two prism will be in the ratio :

7³ : 4³

So, the ratio of volume is 343 : 64.