HOW TO FIND POINT OF INTERSECTION OF TWO CIRCLES

Two prove two circles are intersecting each other at one point, we have to follow the instruction given below.

Step 1 :

Find the centers of the circles. Center of the first and second circles be C₁ and C₂ respectively.

Step 2 :

Find the radius of the circles. Let r₁ and r₂ be radii of circles respectively.

Step 3 :

Distance between centers = Sum of radius 

C₁C₂  = r₁ + r₂

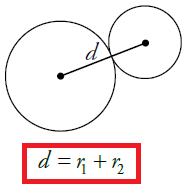
Problem 1 :

Prove that the two circles

x² + y² + 6x - 8y + 9 = 0

and 

x² + y² - 10x + 4y - 7 = 0

just touch each other at single point.

Solution :

x² + y² + 6x - 8y + 9 = 0

x² + 6x + y²- 8y + 9 = 0

(x + 3)² - 3² + (y - 4)²- 4² + 9 = 0

(x + 3)² - 9 + (y - 4)²- 16 + 9 = 0

(x + 3)² + (y - 4)² = 16

Center of the circle C₁(-3, 4) and radius(r₁) = 4

x² + y² - 10x + 4y - 7 = 0

x² - 10x + y²+ 4y - 7 = 0

(x - 5)² - 5² + (y + 2)² - 2² - 7 = 0

(x - 5)² + (y + 2)² = 25 + 4 + 7

(x - 5)² + (y + 2)² = 36

Center of the circle C₂(5, -2) and radius(r₂) = 6

Distance between centers :

C₁(-3, 4) and C₂(5, -2)

= √(5+3)² + (-2-4)²

= √8² + (-6)²

= √64 + 36

= √100

= 10  ---(1)

r₁ = 4 and r₂ = 6

r₁ + r₂ = 4 + 6 ==> 10  ---(2)

Since the distance between center is equal to sum of the radii, the circles touches each other at one point.

Problem 2 :

The line y = 4x + c is a tangent to the circle x² + y² = 17

a) Find the two values of c.

b) For the positive value of c, determine the point of contact of the tangent and a circle.

Solution : 

Since the given line is a tangent for the circle, it should satisfy the condition

c² = a²(1 + m²) ----(1)

Equation of the line is in the form y = mx + c

Equation of circle is in the form x² + y² = a²

a² = 17, m = 4, c = c

Applying these values in (1), we get

c² = 17(1 + 4²)

c² = 17(1 + 16)

c² = 17(17)

c = 17

Problem 3 :

The straight line y = x cuts the circle x² + y² - 6x - 2y - 24 = 0 at A and B

a) Find the coordinates A and B.

b) Find the equation of the circle which has the diameter of the circle

Solution :

The circle and a line  x² + y² - 6x - 2y - 24 = 0 cuts the line y= x

x² + x² - 6x - 2x - 24 = 0

2x² - 8x - 24 = 0

x² - 4x - 12 = 0

(x - 6)(x + 2) = 0

x = 6 and x = -2

y = 6 and y = -2

So, the points are A(6, 6) and B(-2, -2).

Equation of the circle having A and B as endpoints of the diameter,

(x - x₁) (x - x₂) + (y - y₁) (y - y₂) = 0

(x - 6) (x + 2) + (y - 6) (y + 2) = 0

x² - 6x + 2x - 12 + y² - 6y + 2y - 12 = 0

x² + y² - 4x - 4y - 24 = 0