How to Find End Behaviour of Polynomial Functions

The end behavior of a polynomial function is the behavior of the graph of f(x) as x approaches positive infinity or negative infinity.

The degree and the leading coefficient of a polynomial function determine the end behavior of the graph.

The leading coefficient is significant compared to the other coefficients in the function for the very large or very small numbers. So, the sign of the leading coefficient is sufficient to predict the end behavior of the function.

Degree is odd leading coefficient is positive

Considering the function

f(x) = x³

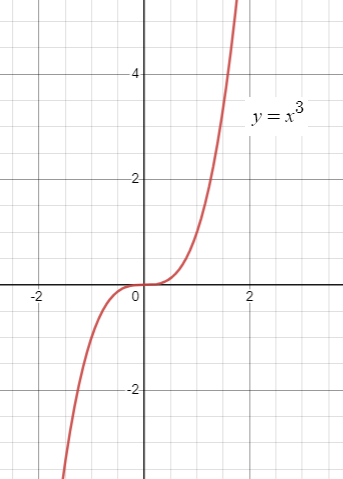
When x -> ∞ then y --> ∞

When x -> -∞ then y --> -∞

Degree is odd leading coefficient is negative

Considering the function

f(x) = -x³

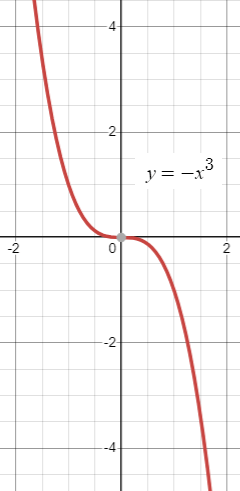
When x -> ∞ then y --> -∞

When x -> -∞ then y --> ∞

Degree is even leading coefficient is positive

Considering the function

f(x) = x²

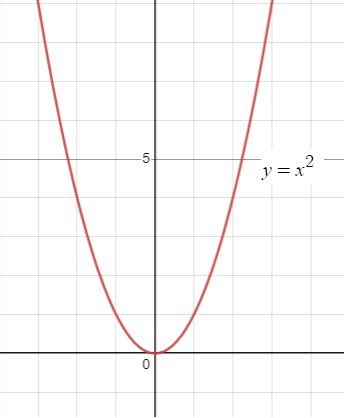
When x -> ∞ then y --> ∞

When x -> -∞ then y --> ∞

Degree is even leading coefficient is negative

Considering the function

f(x) = -x²

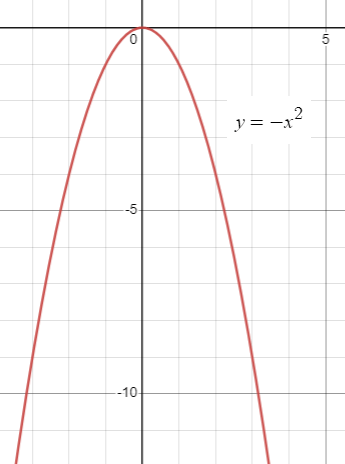
When x -> ∞ then y -->-∞

When x ->-∞ then y -->-∞

Identify the leading coefficient, degree and end behavior.

Problem 1 :

f(x) = 5x² + 7x - 3

Solution :

Degree :

Highest exponent of the polynomial is 2. So, degree is 2.

Leading coefficient :

Coefficient of x² is 5. It is positive.

End behavior :

When x -> ∞ then y --> ∞

When x -> -∞ then y --> ∞

Problem 2 :

f(x) = -2x² - 3x + 4

Solution :

Degree :

Highest exponent of the polynomial is 2. So, degree is 2.

Leading coefficient :

Coefficient of x² is -2. It is negative.

End behavior :

When x -> ∞ then y --> -∞

When x -> -∞ then y --> -∞

Problem 3 :

f(x) = x³ -  9x² + 2x + 6

Solution :

Degree :

Highest exponent of the polynomial is 3. So, degree is 3.

Leading coefficient :

Coefficient of x³ is 1. It is positive 

End behavior :

When x -> ∞ then y --> ∞

When x -> -∞ then y --> -∞

Problem 4 :

f(x) = -7x³  + 3x² + 12x - 1

Solution :

Degree :

Highest exponent of the polynomial is 3. So, degree is 3.

Leading coefficient :

Coefficient of x³ is -7. It is negative.

End behavior :

When x -> ∞ then y --> -∞

When x -> -∞ then y --> ∞

Problem 5 :

f(x) = -2x⁷ + 5x⁴ - 3x

Solution :

Degree :

Highest exponent of the polynomial is 7. So, degree is 7.

Leading coefficient :

Coefficient of x⁷ is -2. It is negative.

End behavior :

When x -> ∞ then y --> -∞

When x -> -∞ then y --> ∞

Problem 6 :

f(x) = 8x³ + 4x² + 7x⁴ - 9x

Solution :

The given polynomial is not arranged in correct order.

f(x) =   7x⁴ + 8x³ + 4x² - 9x

Degree :

Highest exponent of the polynomial is 4. So, degree is 4.

Leading coefficient :

Coefficient of x⁴ is 7. It is positive

End behavior :

When x -> ∞ then y --> ∞

When x -> -∞ then y --> ∞

Problem 7 :

Identify the end behavior. Justify your answer.

f(x) = 4x⁵ - 3x⁴ + 2x³

Solution :

f(x) = 4x⁵ - 3x⁴ + 2x³

Degree :

Highest exponent of the polynomial is 5. So, degree is 5.

Leading coefficient :

Coefficient of x⁵ is 4. It is positive

End behavior :

When x -> ∞ then y --> ∞

When x -> -∞ then y --> -∞

Problem 8 :

Identify the end behavior. Justify your answer.

f(x) = x⁴ + x³ - x²

Solution :

f(x) = x⁴ + x³ - x²

Degree :

Highest exponent of the polynomial is 4. So, degree is 4.

Leading coefficient :

Coefficient of x⁴ is 1. It is positive

End behavior :

When x -> ∞ then y --> ∞

When x -> -∞ then y --> ∞