HOW TO FIND DIAGONAL OF A KITE

To find diagonal, we have the following ways.

(i) From the given area and one diagonal, find the other diagonal.

(ii) Using Pythagorean theorem, find length of diagonal.

The diagonals of a kite are perpendicular to each other. The longer diagonal of the kite bisects the shorter diagonal.

Area of kite ?

A kite is a quadrilateral which has two pairs of adjacent sides equal in length.

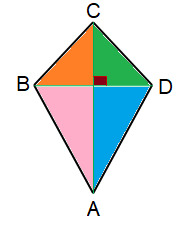
To find area of kite we need diagonals.

Area of kite = (1/2) x diagonal 1 x diagonal 2

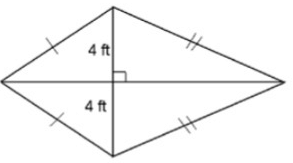
Problem 1 :

The area of this shape is 48 ft². Solve for x. 

Solution :

By observing the figure, length of one diagonal is given.

Area of a kite = 1/2 d₁d₂

Let x be the another diagonal.

48 = 1/2 (8)(x)

48 = 4x

Divide both sides by 4.

48/4 = 4x/4

12 = x

So, the value of x is 12

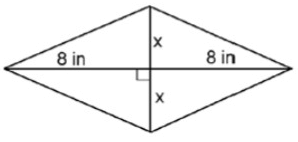
Problem 2 :

The area of this shape is 32 in². Solve for x. 

Solution :

This is a rhombus.

Area of a rhombus = 1/2 d₁d₂

d₁ = 8 + 8 = 16

d₂ = x + x = 2x

32 = 1/2 (16)(2x)

32 = 8(2x)

x = 32/16

x = 2

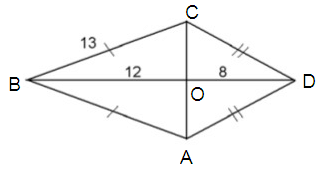
Problem 3 :

Find the area of the kite given below,

Solution :

In kite, the diagonal will bisect each other at right angles.

To figure out OC,

Use Pythagorean Theorem :

(BC)² = (CO)² + (BO)²

(13)² = (CO)² + (12)²

169 = (CO)² + 144

Subtract 144 from both sides.

25 = (CO)²

CO = 5, then CA = 2(5) ==> 10

Area of a kite = 1/2 d₁d₂

 = 1/2 (10)(20)

 = 1/2 (200)

= 100

So, area of a kite is 100.

Problem 4 :

Draw a kite with diagonals of 20 and 24. What is the area of the kite?

Solution :

Area of a kite = 1/2 d₁d₂

 = 1/2 (20)(24)

 = 1/2 (480)

= 240

So, area of a kite is 240.

Problem 5 :

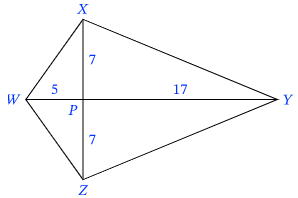
In the kite WXYZ, find length of all sides.

Solution :

Since it is kite, XZ is perpendicular to WY.

XY = ZY and WX = WZ

In triangle XPY,

XY² = XP² + PY²

XY² = 7² + 17²

XY² = 49 + 289

XY = √338

XY = 13√2 and XZ = 13√2

In triangle XWP,

WX² = WP² + PX²

WX² = 5² + 7²

WX² = 25 + 49

WX = √74 and WZ = √74

Problem 6 :

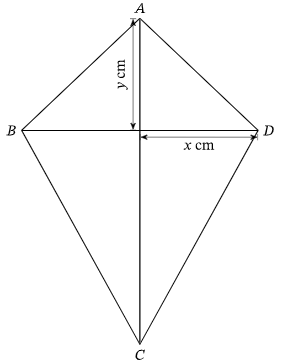
In the kite ABCD, AB = 6 cm, CD = 9 cm and AC = 12 cm.

Solution :

Let E be the point of intersections of two diagonals.

In triangle ABE,

AB = 6

x² + y² = 6² ----(1)

In triangle EDC,

EC² + ED² = CD²

(12 - y)² + x² = 9²----(2)

From (1),

x² = 36 - y² 

Applying the value of x² in (2), we get

144 + y² - 24y + 36 - y² = 81

180 - 24y = 81

-24y = -99

y = 4.125

x² = 36 - (4.125)

x² = 18.98

x = √18.98

x = 4.35