HOW TO FIND DEGREE LEADING COEFFICIENT AND END BEHAVIOR OF POLYNOMIAL

State the degree, leading coefficient, and end behaviours of each polynomial function

Problem 1 :

f(x) = -4x⁴ + 3x² - 15x + 5

Solution :

Degree = 4

Leading coefficient = -4 (negative)

End behavior :

lim x--> ∞, f(X) --> -∞

lim x--> -∞, f(X) --> -∞

Problem 2 :

f(x) = 2x⁵  - 4x³ + 10x² - 13x + 8

Solution :

Degree = 5

Leading coefficient = 2 (positive)

End behavior :

lim x--> ∞, f(X) --> ∞

lim x--> -∞, f(X) --> -∞

Problem 3 :

f(x) = 4 - 5x + 4x²  - 3x³

Solution :

f(x) = 4 - 5x + 4x²  - 3x³

Writing the polynomial in standard form, we get

f(x) = - 3x³ + 4x² - 5x + 4

Degree = 3

Leading coefficient = -3 (negative)

End behavior :

lim x--> ∞, f(X) --> -∞

lim x--> -∞, f(X) --> ∞

Problem 4 :

f(x) = 2x(x - 5)(3x + 2)(4x - 3)

Solution :

f(x) = 2x(x - 5)(3x + 2)(4x - 3)

= 2x(3x² + 2x - 15x - 10)(4x - 3)

= 2x(3x² - 13x - 10)(4x - 3)

= 2x (12x³ - 3x² - 52x + 39x - 40x + 30)

= 2x (12x³ - 3x² - 53x + 30)

= 24x⁴ - 6x³ - 106x² + 30x

Degree = 4

Leading coefficient = 24 (positive)

End behavior :

lim x--> ∞, f(X) --> ∞

lim x--> -∞, f(X) --> ∞

For each of the following graphs, decide if

a) the function has an even or odd degree

b) the leading coefficient is positive or negative

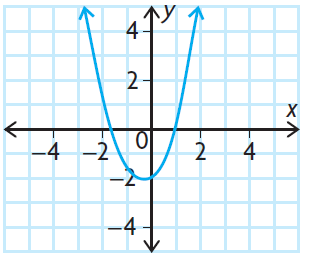
Problem 5 :

Solution :

Observing the end behavior from the given graph,

lim x -> ∞, f(x) -> -∞

lim x -> -∞, f(x) -> -∞

The graphical form of the given function shows that, it must even degree polynomial with negative leading coefficient.

a) even degree

b) negative leading coefficient

Problem 6 :

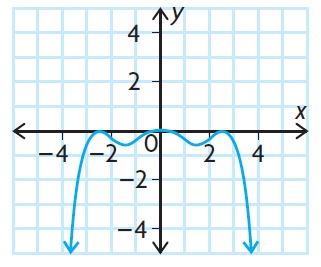
Solution :

Observing the end behavior from the given graph,

lim x -> ∞, f(x) -> -∞

lim x -> -∞, f(x) -> -∞

The graphical form of the given function shows that, it must even degree polynomial with negative leading coefficient.

a) even degree

b) negative leading coefficient

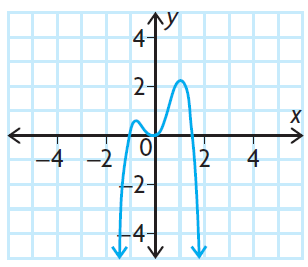
Problem 7 :

Solution :

Observing the end behavior from the given graph,

lim x -> ∞, f(x) -> -∞

lim x -> -∞, f(x) -> ∞

The graphical form of the given function shows that, it must odd degree polynomial with negative leading coefficient.

a) odd degree

b) negative leading coefficient

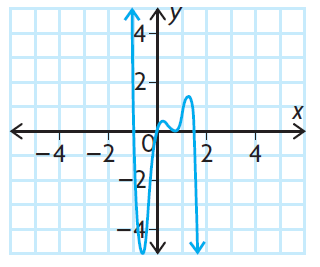
Problem 8 :

Solution :

Observing the end behavior from the given graph,

lim x -> ∞, f(x) -> ∞

lim x -> -∞, f(x) -> ∞

The graphical form of the given function shows that, it must even degree polynomial with positive leading coefficient.

a) even degree

b) positive leading coefficient

Problem 9 :

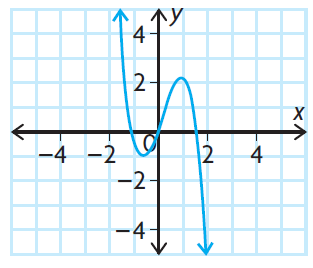
Solution :

Observing the end behavior from the given graph,

lim x -> ∞, f(x) -> -∞

lim x -> -∞, f(x) -> ∞

The graphical form of the given function shows that, it must odd degree polynomial with negative leading coefficient.

a) odd degree

b) negative leading coefficient

Problem 10 :

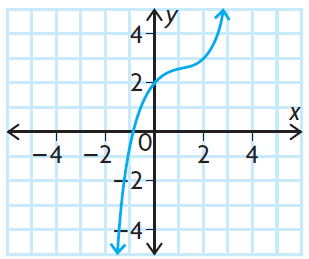
Solution :

Observing the end behavior from the given graph,

lim x -> ∞, f(x) -> ∞

lim x -> -∞, f(x) -> -∞

The graphical form of the given function shows that, it must odd degree polynomial with positive leading coefficient.

a) odd degree

b) positive leading coefficient

Problem 11 :

f is a polynomial function of degree n, where n is a positive even integer. Decide whether each of the following statements is true or false. If the statement is false, give an example that illustrates why it is false.

a) f is an even function.

b) f cannot be an odd function.

c) f will have at least one zero.

d) As x -> ∞, y -> ∞ and as x -> ∞, y -> ∞

Solution :

a) f is an even function.

Since it is even degree polynomial, it must not be even function. So, the given statement is false.

For example, let us cosider two polynomials of even degree. To check if the function is even or odd, we have to check the conditions,

• f(-x) = f(x) --> even function
• f(-x) = -f(x) --> odd function
• Otherwise it is neither

b) f cannot be an odd function.

From the above proof, we cannot decide it is odd or even. So, the statement is false.

c) f will have at least one zero.

• Even degree polynomial with positive coefficient will start with second quadrant and ends with first quadrant.
• Even degree polynomial with negative coefficient will start with third quadrant and ends with fourth quadrant.

Even degree polynomial may not have zero, there may not be x-intercepts. So, this statement is false.

d) As x -> ∞, y -> ∞ and as x -> -∞, y -> ∞

By analyzing the end behavior, it is true.