HOW TO FIND CUBE ROOT OF A NUMBER

Evaluate :

Problem 1:

∛1

Solution :

∛1 = 1

Problem 2 :

∛-1

Solution :

∛-1 = ∛(-1) ⋅ (-1) ⋅ (-1)

= -1

Problem 3 :

∛-27

Solution :

∛-27

We can write 27 as 3 × 3 × 3,

∛-27 = ∛(-3 × -3 × -3)

∛-27 = -3

Problem 4 :

∛8

Solution :

∛8

We can write 8 as 2 × 2 × 2,

∛8 = ∛2 × 2 × 2

∛8 = 2

Problem 5 :

∛-8

Solution :

∛-8

We can write 8 as 2 × 2 × 2,

∛-8 = ∛(-2 × -2 × -2)

∛-8 = -2

Problem 6 :

∛64

Solution :

∛64

We can write 64 as 4 × 4 × 4,

∛64 = 4 × 4 × 4

∛64 = 4

Problem 7 :

∛125

Solution :

∛125

We can write 125 as 5 × 5 × 5,

∛125 = 5 × 5 × 5

∛125 = 5

Problem 8 : 

∛-216

Solution :

∛-216

We can write 216 as 6 × 6 × 6,

∛-216 = ∛(-6 × -6 × -6)

∛-216 = -6

Problem 9 :

∛-1000

Solution :

∛-1000

We can write 1000 as 10 × 10 × 10,

∛-1000 = ∛(-10 × -10 × -10)

∛-1000 = -10

Problem 10 :

∛343

Solution :

∛343

We can write 343 as 7 × 7 × 7,

∛343 = 7 × 7 × 7

∛343 = 7

Problem 11 :

Find the value of the cube roots

∛(27 x 2744)

Solution :

∛(27 x 2744) = ∛27 x ∛2744

Decomposing each number as product of prime factors, we get

= ∛(3 x 3 x 3) x ∛(2 x 2 x 2 x 7 x 7 x 7)

For every three same numbers, we have to take one out of the cube root.

= 3 x 2 x 7

= 42

Problem 12 :

By which smallest number must 5400 be multiplied to make it a perfect cube?

Solution :

Here 5400 is not a perfect cube, by multiplying 5400 by some number it can be converted into perfect cube. To find the required number, we start with prime factorization.

= ∛(2 x 2 x 2 x 3 x 3 x 3 x 5 x 5)

Here we see three 2's and three 3's, since we have two 5's we cannot take one out. Then 5 is the number to be multiplied to make it as perfect cube.

Problem 13 :

Find the smallest number by which 16384 be divided so that the quotient may be a perfect cube.

Solution :

From the given number 16384 is not a perfect cube, inorder to make it as perfect cube we have to divide 

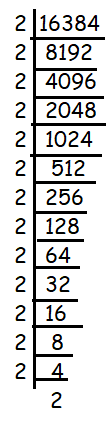
= ∛(2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2)

By grouping three same values, we have two 2's extra and that should be ignored. So, the required number to be divided is 4.

Problem 14 :

Is 4096 a perfect cube? If yes, then what is the number whose cube root is 4096?

Solution :

To check if the given number 4096 is a perfect cube or root, we try to express the given number as the product of prime factors.

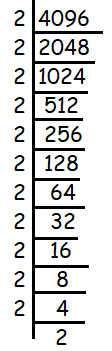
= ∛(2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2)

For every three same values, we are able to take one value out of the cube root. Then,

= 2 x 2 x 2 x 2

= 12

Since we dont have any left over inside the cube root sign, it must be the perfect cube.

Problem 15 :

Find the smallest number by which 375 must be multiplied to obtain a perfect cube

Solution :

From the given information, it is clear that 375 is not a perfect cube. To make it as perfect cube, we have to multiply 375 by a number. That least value can be figured it out simply while writing the given number as product of prime factors.

375 = ∛(5 x 5 x 5 x 3)

Here we see one 3, to make it as group we need two more 3's. So, the required number to be multiplied in order to make it as perfect cube is 9.

Problem 16 :

Find the cube root of 0.008/0.125

Solution :

= ∛0.008/0.125

Using the properties of radial, we use the cube root for both numerator and denominator separately.

= ∛0.008/∛0.125

∛0.008 = ∛(8/1000)

= ∛(2 x 2 x 2)/(10 x 10 x 10)

= 2/10

∛0.125 = ∛(0.125 x 1000/100)

= ∛(125/1000)

= ∛(5 x 5 x 5)/(10 x 10 x 10)

= 5/10

Dividing these two fractions, we get

= 2/10 / (5/10)

= 2/10 x 10/5

= 2/5

= 0.4