FINDING CRITICAL POINTS

To find critical numbers, we have to use steps given below.

Step 1 :

Find the first derivative.

Step 2 :

Equate the first derivative to 0.

Step 3 :

Solve for the variable. From this, we can understand that slope will be zero at these positions.

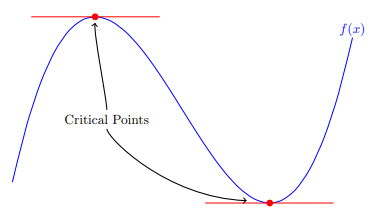
Use Calculus to find the CRITICAL POINTS of each of the following functions:

Problem 1 :

f(x) = 3x² - 5x + 1

Solution :

Let f(x) = 3x² - 5x + 1

f'(x) = 6x - 5 + 0

f'(x) = 6x - 5

f'(x) = 0

6x - 5 = 0

2x = 5

x = 5/6

The curve will flatten at the x-coordinate 5/6. So, the critical number is at x = 5/6.

Problem 2 :

f(x) = x⁴ + 2x³ - 1

Solution :

f(x) = x⁴ + 2x³ - 1

f'(x) = 4x³ + 2(3x²) - 0

f'(x) = 4x³ + 6x²

f'(x) = 0

4x³ + 6x² = 0

2x²(2x + 3) = 0

2x² = 0 and 2x + 3 = 0

x = 0 and x = -3/2

So, the critical points are 0 and -3/2

Problem 3 :

f(x) = (8x - 16) / x²

Solution :

f(x) = (8x - 16) / x²

Using quotient rule, we find the first derivative.

f'(x) = (vu' - uv') / v²

= (x²(8) - (8x - 16)(2x)) / (x²)²

= (8x²- (16x² - 32x)) / x⁴

= (8x²- 16x² + 32x) / x⁴

f'(x) = (-8x² + 32x) / x⁴

f'(x) = 0

(-8x² + 32x) / x⁴ = 0

-8x² + 32x = 0

-4x(2x - 8) = 0

4x = 0 and 2x - 8 = 0

x = 0 and 2x = 8 ==> x = 4

So, the critical points are 0 and 4.

Problem 4 :

f(x) = 2x + 3x^2/3

Solution :

f(x) = 2x + 3x^2/3

f'(x) = 2(1) + 3(2/3)x^{(2/3) - 1}

f'(x) = 2 + 2x^(-1/3)

f'(x) = 0

2 + 2x^(-1/3) = 0

2x^(-1/3) = -2

x^(-1/3) = -1

1/∛x = -1

∛x = -1

x = -1

So, the critical point is at x = -1.

Problem 5 :

f(x) = x⁴ - 2x² + 3

Solution :

f(x) =  x⁴ - 2x² + 3

f'(x) = 4x³ - 2(2x) + 0

= 4x³ - 4x

f'(x) = 0

4x³ - 4x = 0

4x(x² - 1) = 0

4x = 0 and x² - 1 = 0

x = 0 and x² = 1

x = 1 and -1

So, the critical points are -1, 0 and 1.